Abstraction des données

L'abstraction des données est une technique de programmation (qui n'est pas propre à la programmation fonctionnelle) et qui consiste à manipuler des données définies de manière abstraite indépendamment de la façon dont elles sont implantées.

14. Types abstraits de données

Pour bien programmer un problème, on doit passer par plusieurs étapes :

Étant donné la spécification d'un problème, la première phase consiste en une analyse du problème qui permet de définir les algorithmes permettant de le résoudre. La phase de codage n'intervient qu'après la définition des algorithmes et après avoir choisi un langage de programmation.

La phase d'analyse fait apparaître une certain nombre de classes d'objets que l'on va devoir manipuler ainsi que les opérations qui leurs sont associées. Par exemple des ensembles et les opérations d'union, d'intersection, etc... ou bien des listes et les opérations élémentaires cons, car, cdr.

Ce sont ces classes d'objets qui constituent des types abstrait de données .

Un type de données peut être prédéfini dans le langage de programmation utilisé, auquel cas on parle de type de base.

Ex :

-

les entiers et les opérations +, -, *, /, = ... associées

-

les booléens et les opérations and, or, not, ...

-

les listes en Scheme et les opérations cons, car et cdr

Si c'est un type que l'on définit, on parle de type abstrait de données (TAD).

14.1 Comment définit-on un TAD ?

On définit un type de données abstrait $\cal T$ en décrivant le profil des fonctions pour lesquelles le type $\cal T$ entre en jeu. Ces fonctions admettent un certain nombre (éventuellement 0) de paramètres et fournissent un résultat. Le profil d'une fonction doit faire apparaître les types des paramètres et du résultat :

$$f : T_1, T_2, \ldots T_n \longrightarrow T_{n+1}$$

On peut diviser les fonctions d'un TAD en deux classes (pas forcément disjointes) :

-

les fonctions où le type $\cal T$ apparaît comme type d'un paramètre

-

les fonctions où $\cal T$ apparaît comme type du résultat

Les autres types apparaissant dans le profil des fonctions sont supposés déjà définis.

Parmi les fonctions dont le résultat est de type $\cal T$, on distingue celles qui permettent d'engendrer tous les objets de type $\cal T$ et que l'on appelle fonctions génératrices de $\cal T$.

De même parmi les fonctions dont un des paramètres est de type $\cal T$ on en distingue certaines que l'on appelle fonctions caractéristiques de $\cal T$.

Les génératrices et les caractéristiques forment un ensemble minimal de fonctions à partir desquelles on définit toutes les autres fonctions opérant sur ou dans $\cal T$.

On peut spécifier des axiomes liant ces fonctions, ce qui permet de démontrer des propriétés de programme.

Ex :

On définit le TAD $\cal L$ des listes plates finies d'entiers de la manière suivante :

génératrices de $\cal L$	$\left\{\begin{array}{lcccc} \mbox{liste-vide}& : & & \rightarrow & {\cal L}\\ ... ... \hbox{I\hskip -1.8pt N}, {\cal L} & \rightarrow & {\cal L} \end{array}\right.$
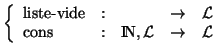caractéristiques de $\cal L$	$\left\{\begin{array}{lcccc} \mbox{car~~~~~~~}& : & {\cal L} & \rightarrow & \h... ...t N}\\ \mbox{cdr} & : & {\cal L} & \rightarrow & {\cal L} \end{array}\right.$

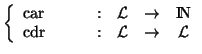Axiome : $\forall x \neq \mbox{ liste-vide} : x=cons(car(x), cdr(x))$

14.2 Utilisation d'un TAD

Quand on utilise un TAD on ne prend pas en compte les détails de son implantation. En d'autres termes, les algorithmes résultant de l'analyse de la spécification utilisent uniquement les fonctions génératrices et caractéristiques et les autres fonctions relatives au TAD $\cal T$.

Le programme résultant du codage respecte l'abstraction des données, c'est à dire qu'on distingue bien deux parties :

-

une partie correspondant au codage des algorithmes où l'on n'utilise que les génératrices, caractéristiques et fonctions du TAD

-

une autre partie (un module, un autre fichier) où les fonctions du TAD sont effectivement implantées à l'aide des types dont on dispose déjà (types de bases et TAD précédemment définis)

Cette technique de programmation offre deux avantages :

1.

Les programmes sont plus clairs car ils se focalisent sur la manière de résoudre un problème. On ne mélange pas les choix d'implantation et l'étude des algorithmes.

2.

Le codage des algorithmes étant complètement indépendant de l'implantation des données, les programmes restent valident même si on décide de changer complètement l'implantation.

14.3 Un exemple : le TAD doublet

On définit le TAD doublet (d'entiers naturels) dont les profils des fonctions génératrices et caractéristiques sont :

cons-doublet : $\hbox{I\hskip -1.8pt N}, \hbox{I\hskip -1.8pt N}\rightarrow {\cal D}$

premier : ${\cal D} \rightarrow \hbox{I\hskip -1.8pt N}$

second : ${\cal D} \rightarrow \hbox{I\hskip -1.8pt N}$

Avec l'axiome :

$$\forall d\in{\cal D} : d=\mbox{cons-doublet}(\mbox{premier}(d), \mbox{second}(d))$$

Connaissant le profil de ces fonctions, on peut écrire un programme utilisant le TAD doublet qui est complètement indépendant de toute implantation ;

; programme utilisant le TAD doublet

 (define symetrique (lambda (d)
    (cons-doublet (second d) (premier d))))

 (define egal-doublet? (lambda (d1 d2)
    (and (= (premier d1) (premier d2))
         (= (second d1) (second d2)) ))

Et voici deux implantations possibles du TAD doublets :

; 1ere implantation fondee sur les listes

  (define cons-doublet 
     (lambda (a b)(list a b)) )

  (define premier 
     (lambda (d) (car d)))

  (define second
     (lambda (d) (cadr p)))

; 2eme implantation fondee sur les entiers

  (define cons-doublet 
     (lambda (a b) (* (expt 2 a) (expt 3 b)) ))

  (define premier (lambda (d)
     (define premier-aux
          (lambda (d1 n)
             (let ( (q (quotient d1 2))
                    (r (remainder d1 2)) )
                  (if (not (= r 0))
                      n
                      (premier-aux q (+ n 1))))))
     (premier-aux d 0) ))

  (define second (lambda (d)
     (define second-aux 
        (lambda (d1 n)
            (let ( (q (quotient d1 3))
                   (r (remainder d1 3)) )
                 (if (not (= r 0))
                     n
                     (second-aux q (+ n 1))))))
        (second-aux d 0) ))

14.4 Deux TAD classiques : les piles et les files

14.4.1 Les piles d'entiers

pile-vide  :   $\quad \rightarrow {\cal P}$

empiler  :   $\hbox{I\hskip -1.8pt N},{\cal P} \rightarrow {\cal P}$

sommet  :   ${\cal P} \rightarrow \hbox{I\hskip -1.8pt N}$

depiler  :   ${\cal P} \rightarrow \hbox{I\hskip -1.8pt N}$

pile-vide?  :   ${\cal P} \rightarrow {\cal B}$

Implantation à l'aide de listes :

      (define pile-vide 
        (lambda () '()))

      (define empiler
         (lambda (x p) (cons x p)))

      (define sommet
         (lambda (p) (car p)))

      (define depiler
         (lambda (p) (cdr p)))

     (define pile-vide?
         (lambda (p) (equal? p '())))

14.4.2 Les files d'entiers

file-vide  :   $\quad \rightarrow {\cal F}$

enfiler  :   $\hbox{I\hskip -1.8pt N},{\cal F} \rightarrow {\cal F}$

tete  :   ${\cal F} \rightarrow \hbox{I\hskip -1.8pt N}$

defiler  :   ${\cal F} \rightarrow \hbox{I\hskip -1.8pt N}$

file-vide?  :   ${\cal F} \rightarrow {\cal B}$

Implantation à l'aide de listes :

      (define file-vide
          (lambda (f) '()))

      (define enfiler
         (lambda (x f) (append f (cons x '())) ))

      (define tete
         (lambda (f) (car f)))

      (define defiler
         (lambda (f) (cdr f)))

     (define file-vide?
         (lambda (f) (equal? f '())))