Notion de complexité

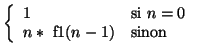Écrire une fonction qui ``marche'' ne suffit pas forcément pour résoudre un problème. La difficulté est aussi de le faire efficacement.

Pour juger de l'efficacité d'une fonction, on s'intéresse aux liens qui existent entre le texte de la fonction et le processus engendré à l'intérieur de l'interprète Scheme lors de l'évaluation de l'application de cette fonction.

On veut évaluer en particulier :

-

le temps consommé pour évaluer l'expression = la complexité en temps

-

l'espace mémoire utilisé = la complexité en espace

Le but est de disposer de critères qualitatifs :

-

de comparaison d'algorithmes pour un problème donné

-

d'évaluation de la complexité intrinsèque d'un problème

10. Un exemple de comparaison d'algorithmes

Le problème est de programmer une fonction qui calcule la factorielle d'un nombre donné.

10.1 Une première version

En partant de 0!=1 et n!=(n-1)! * n, on peut spécifier le problème de la manière suivante :

f1 :	Entier	$\longrightarrow$	Entier
	n	$\longmapsto$	$\left\{ \begin{array}{ll} 1 & \mbox{si } n=0\\ n * \mbox{ f1}(n-1) & \mbox{sinon} \end{array}\right.$

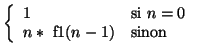En traduisant directement en Scheme, on obtient la fonction :

      (define f1
         (lambda (n)
            (if (= n 0)
                1
                (* n (f1 (- n 1))) )))

10.2 Une autre version

On peut aussi écrire $n! = 1 \times 2 \times 3 \times \ldots \times n$ et donc effectuer le calcul à l'aide d'un compteur C qui varie de 1 jusqu'à n et d'un paramètre accumulateur PC où l'on conserve le résultat courant :

$PC\longleftarrow 1$
$C \longleftarrow 1$
tant que $c\leqslant n$ faire
$PC \longleftarrow PC \times C$
$C \longleftarrow C + 1$

Cet algorithme se traduit en Scheme en utilisant une fonction auxiliaire dont les arguments sont le compteur et le paramètre accumulateur :

f2 :	Entier	$\longrightarrow$	Entier
	n	$\longmapsto$	f2-aux(1, 1)
f2-aux :	Entier, Entier	$\longrightarrow$	Entier
	C, PC	$\longmapsto$	$\left\{ \begin{array}{ll} PC & \mbox{si } C>n\\ \mbox{ f2-aux}(C+1, PC*C) & \mbox{sinon} \end{array}\right.$

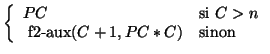      (define f2 
         (lambda (n)
            (define f2-aux 
               (lambda (C PC)
                   (if (> C n)
                    PC
                   (f2-aux (+ C 1) (* PC C)) )))
            (f2-aux 1 1) ))

10.3 Comparons l'exécution des deux fonctions

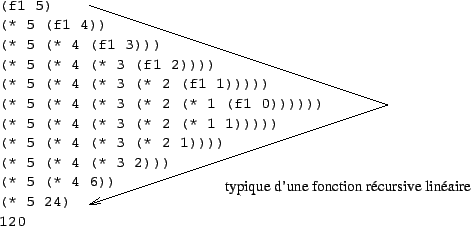
Examinons dans les deux cas comment évolue l'expression à évaluer lorsqu'on veut calculer n!:

Pour la première version on obtient :

Et pour la seconde version :

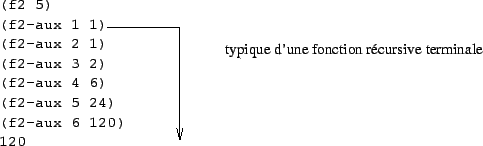
On constate que :

• l'évaluation avec la première version est plus longue, elle nécessite plus de calculs;
• avec la première version l'évaluation se fait en deux étapes, d'abord l'expression à évaluer ``grandit'' au fur et à mesure des appels récursifs jusqu'à atteindre la condition d'arrêt, puis elle diminue au fur et à mesure qu'elle est évaluée par l'interprète;
• au contraire, avec la deuxième version la taille de l'expression reste constante et le nombre d'étapes est moins élevé.

Évaluation de la complexité des deux fonctions :

La trace de l'évaluation avec la première version est caractéristique d'une récursivité linéaire, le nombre d'étapes de calcul (le temps de calcul) est proportionnel à n, et l'espace nécessaire en mémoire (la taille maximale de l'expression) est aussi proportionnelle à n.

Pour la seconde version, le temps de calcul est aussi proportionnel à n, en revanche l'espace nécessaire en mémoire est constant. Cela est caractéristique d'une récursivité terminale : une fois que tous les appels récursifs sont effectués le calcul est terminé.

Remarque : Avec DrScheme, on peut obtenir la trace de l'évaluation d'une fonction. Pour cela il est nécessaire de charger dans l'interprète une librairie où est définie la fonction trace. Ce chargement s'effectue en ajoutant au début du programme l'expression : (require-library "trace.ss"). On l'utilise de la manière suivante :

(trace <nom_de_fonction>) : force l'interprète à tracer une fonction

(untrace <nom_de_fonction>) : pour que l'interprète ne trace plus la fonction

11. Notation pour la complexité

Le but de l'étude de la complexité d'une fonction est de donner un ordre de grandeur du temps de calcul et/ou de l'espace mémoire utilisé en fonction d'une mesure des données.

Plus formellement, pour évaluer la complexité en temps d'un programme on ne compte pas le nombre de ligne de la trace mais on dénombre la ou les opérations qui sont fondamentales pour résoudre le problème.

Dans le cas de fonctions récursives, ce dénombrement consiste le plus souvent à résoudre des équations de récurrence (suites arithmétiques, géométriques).

Souvent, on utilisera les mesures suivantes sur les données que manipule une fonction :

-

pour un entier n, la mesure est n

-

pour une liste, la mesure est la longueur de la liste

-

pour un couple d'entiers (n, p), selon le code de la fonction, la mesure pourra être : n ou p ou n+p ou n*p

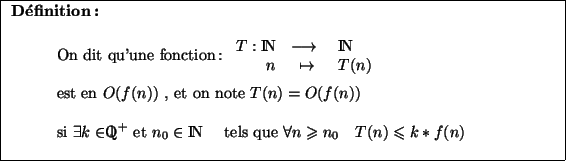
Ex :

La fonction constante $n\mapsto 2$ est en O(n³), en O(n), en $O(\log_2(n))$ et plus précisément en O(1).

$n\mapsto n^2+3n+3708$ est en O(n²)

$n\mapsto n^{50}+2^n$ est en O(2ⁿ)

$n\mapsto n$ n'est pas en $O(\log_2(n))$
En pratique, étant donné le code d'une fonction :

(define f (lambda (p₁ ...p_m) <expr>))

où les p_i sont à valeur dans $\hbox{I\hskip -1.8pt D}_i$, déterminer la complexité en temps de f, c'est choisir la <<bonne>> mesure : $M : \hbox{I\hskip -1.8pt D}_1, \hbox{I\hskip -1.8pt D}_2, \hbox{I\hskip -1.8pt D}_m \rightarrow \hbox{I\hskip -1.8pt N}$ telle que le nombre d'opérations fondamentales nécessaires au calcul de (f p₁ ... p_m) soit en $O(g(M(p_1 \ldots p_m)))$ avec g suffisamment <<simple>> et <<précise>> !

12. Un exemple de récursivité quadratique

On s'intéresse au problème du renversement d'une liste sans utiliser la fonction prédéfini append.

Pour renverser une liste non vide, on a déjà vu qu'il suffit de renverser le reste de la liste et d'ajouter le premier élément à la fin du résultat. Pour résoudre le problème, on a donc besoin de deux fonctions renverse et ajoutefin qu'on peut spécifier par :

ajoutefin	Objet, Liste	$\longrightarrow$	Liste
	o, l	$\longmapsto$	$\left\{ \begin{array}{ll} (o) & \mbox{si } l \mbox{ est vide}\\ (x\ .\ ajoutefin(o, l')) & \mbox{sinon, avec {\em l=(x . l')}} \end{array}\right.$
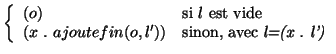renverse :	Liste	$\longrightarrow$	Liste
	l	$\longmapsto$	$\left\{ \begin{array}{ll} liste vide & \mbox{si } l \mbox{ est vide}\\ ajoutefin(x, renverse(l') ) & \mbox{sinon, avec {\em l=(x . l')}} \end{array}\right.$

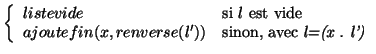Le code Scheme correspondant est le suivant :

      (define ajoutefin
         (lambda (o l)
             (if (null? l)
                 (cons o '())
                 (cons (car l) (ajoutefin o (cdr l))))))

      (define renverse
         (lambda (l)
             (if (null? l)
                 l
                 (ajoutefin (car l) (renverse (cdr l))))))

On veut évaluer la complexité en temps de la fonction renverse en fonction de la longueur de la liste à renverser (c'est la seule donnée de la fonction).

Notons n la longueur de la liste à renverser, il faut calculer le temps consommé par renverse pour une liste de longueur n.

Si on examine la fonction renverse, on voit qu'elle fait appel à la fonction ajoutefin, par conséquent la performance de cette fonction est liée à celle de la fonction ajoutefin dont nous devons d'abord évaluer la complexité.

On voit que le temps consommé pour ajouter un objet à la fin d'une liste ne dépend pas de l'objet en question, on cherche donc à évaluer ce temps en fonction de la longueur de la liste.

On pourrait chronométrer le temps d'évaluation de ajoutefin pour des listes de différentes longueurs mais ce temps dépendrait entre autre de la vitesse de la machine utilisée.

On pourrait tracer l'évaluation, compter le nombre de lignes de la trace et donner un ordre de grandeur. Mais ce n'est pas toujours évident de trouver la relation entre le nombre de lignes et la longueur de la liste.

Pour évaluer la complexité en temps on va calculer le nombre d'opérations fondamentales nécessaires pour résoudre le problème. Ici, l'opération fondamentale est l'opération cons.

Complexité de ajoutefin :

Notons A(p) le nombre d'opérations cons nécessaires pour ajouter un objet à la fin d'une liste de longueur p.

• Si la liste est vide, le résultat est immédiat et on a A(0)=1.

• Si la liste n'est pas vide, on doit évaluer l'expression (cons (car l) (ajoutefin o (cdr l))), on a donc A(p)=1+A(p-1) puisqu'on rappelle la fonction ajoutefin sur le reste de la liste qui est de longueur p-1.

Le nombre d'opérations cons est donc donné par la suite arithmétique A(p), de premier terme 1 et de raison 1. On a donc A(p)=p+1; la complexité de ajoutefin est donc O(p) où p désigne la taille de la liste donnée en argument.

Complexité de renverse :

Notons R(n) le nombre d'opérations cons nécessaires pour renverser une liste de longueur n.

• Si la liste et vide, le résultat est immédiat et on a R(0)=0.
• Sinon il faut évaluer l'expression (ajoutefin (car l) (renverse (cdr l))) qui nécessite un appel à renverse avec une liste de longueur n-1 et un appel à ajoutefin avec une liste de longueur n-1. On a donc R(n)=R(n-1)+A(n-1), c'est à dire R(n)=R(n-1)+n.

On a donc :

R(0)	= 0
R(1)	= R(0) + 1 = 1
R(2)	= R(1) + 2 = 1 + 2
R(3)	= R(2) + 3 = 1 + 2 + 3
...
R(n)	$= R(n-1) + n = \sum_{i=1}^{n} i$

Renverser un liste de longueur n nécessite donc $R(n)=\frac{n(n+1)}{2}$ opérations cons (cela se démontre par récurrence). La complexité en temps de la fonction renverse est donc O(n²).

13. Un exemple de récursivité arborescente

On donne la définition de la suite de Fibonacci :

fib :	Entier	$\longrightarrow$	Entier
	n	$\longmapsto$	$\left\{ \begin{array}{ll} 0 & \mbox{ si {\em n=0}}\\ 1 & \mbox{ si {\em n=1}} \\ fib(n-2)+fib(n-1) & \mbox{ si }n\geq 2 \end{array}\right.$

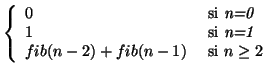Fonction Scheme inspirée directement de la définition :

      (define fib 
         (lambda (n)
            (cond ((= n 0) 0)
                  ((= n 1) 1)
                  (else (+ (fib (- n 1))
                           (fib (- n 2)))) )))

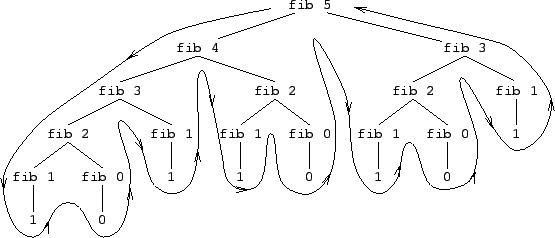
Dans le corps de cette fonction, on effectue deux appels récursifs. Le processus de calcul n'est pas linéaire mais arborescent. Par exemple, l'arbre d'évaluation du calcul de (fib 5) est :

Complexité :

Notons A(n) le nombre d'additions nécessaires pour calculer fib(n). On a :

A(0)	= 0
A(1)	= 0
A(n)	= A(n-1) + A(n-2) + 1

Si on pose F(n)=A(n)+1, on obtient :

F(0)	= 1
F(1)	= 1
F(n)	= A(n) + 1 = A(n-1)+A(n-2)+2
	= F(n-1)+F(n-2)

On retrouve la suite de Fibonacci : F(n)=fib(n+1) et finalement le nombre d'additions est A(n)=fib(n+1)-1.

Pour n grand, on connaît une approximation de la suite de Fibonacci : $fib(n) \approx \frac{\phi^n}{\sqrt 5}$ où $\phi=\frac{1+\sqrt 5}{2}\approx 1.618$ est le nombre d'or.

Le nombre d'additions nécessaire au calcul de (fib n) croît de manière exponentielle avec n, la complexité de cette fonction est exponentielle en $O(\phi^n)$.

Une idée pour élaborer un code Scheme plus efficace :

L'idée consiste à utiliser deux paramètres a et b, initialisés respectivement à 0 et 1 et à appliquer n-1 fois la transformation :

$$\left\vert\begin{array}{l} c \leftarrow a;\\ a \leftarrow a + b;\\ b \leftarrow c \end{array}\right.$$

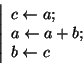
Questions :

-

Quelles sont les valeurs finales de a et b ?

-

Écrire le code Scheme correspondant

-

Évaluer la complexité en temps et en espace de cette fonction