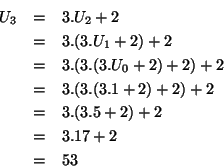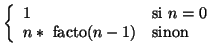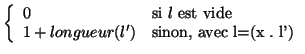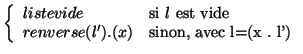

Next: Notion de complexité
Up: No Title
Previous: Les listes
Sous-sections
Les langages de programmation fonctionnelle offrent un style de programmation dans lequel l'itération n'existe pas. Ce mécanisme est remplacé par la récursivité.
La récursivité est fortement liée à la notion de récurrence en mathématiques.
On définit par récurrence la suite U de la manière suivante :
C'est une définition récursive car un terme quelconque Ui est calculé en fonction du terme précédent Ui-1.
Attention, cette définition n'a de sens que si on définit explicitement le terme U0.
On calcule un terme quelconque de cette suite de la manière suivante :
On distingue deux phases dans ce calcul :
- 1.
- on remplace les expressions Ui successivement jusqu'à arriver à U0
- 2.
- on effectue les calculs en commençant par l'expression la plus profonde et en remontant.
On peut énoncer informellement le principe de récurrence de la manière suivante:
C'est ce principe que l'on utilise pour écrire des fonctions récursives.
On définit une fonction récursive permettant de calculer un terme quelconque de la suite U en s'inspirant directement de la définition par récurrence de la suite
(define suite-U
(lambda (n)
(if (= n 0)
1
(+ (* 3 (suite-U (- n 1))) 2) )))
- 1.
- Quel paramètre caractérise la taille du problème ?
Ce paramètre va constituer la variable d'induction.
- 2.
- Quelle est la taille init du problème pour laquelle la solution est triviale et quelle est cette solution ?
La taille init va constituer la condition d'arrêt de la fonction récursive.
- 3.
- Si on connaît la solution du problème pour une taille donnée, quel calcul simple appliqué à cette solution permet de trouver la solution du problème pour une taille supérieure ?
- 4.
- Comment faire varier la variable d'induction pour que celle-ci se rapproche de plus en plus de la valeur init ? Cela afin d'atteindre la condition d'arrêt en un nombre fini d'appels.
Une fois que l'on a les réponses à ces quatre questions, l'écriture de la fonction récursive devient très simple.
Exemple :
Problème : calculer la factorielle d'un nombre n.
- 1.
- taille du problème : le nombre n, variable d'induction : n
- 2.
- taille init : n=0, et solution : n!=1
- 3.
- connaissant (n-1)!, on a
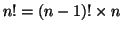
- 4.
- on fait décrémenter n à chaque appel récursif
On peut ainsi donner la spécification de la fonction à écrire :
Et traduire en Scheme :
(define facto
(lambda (n)
(if (= n 0)
1
(* n (facto (- n 1)))) ))
Par définition, les listes sont des structures récursives. Une liste est :
- -
- soit la liste vide
'()
- -
- soit composée d'un premier élément : le
car
et d'une liste : le cdr
Cette nature récursive fait que la plupart des problèmes concernant des listes se résolvent par des fonctions récursives.
On aura souvent (mais ceci n'est pas systématique !) :
- 1.
- taille du problème : la longueur de la liste a traiter,
et variable d'induction : la liste elle-même
- 2.
- condition d'arrêt : si la liste est vide
- 3.
- connaissant le résultat de la fonction sur le reste de la liste, on en déduit la solution pour la liste entière
- 4.
- on fait décroître la taille du problème en appelant récursivement la fonction sur le reste de la liste
Ex :
Calcul de la longueur d'une liste L :
| longueur : |
Liste |
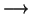 |
Entier |
| |
l |
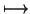 |
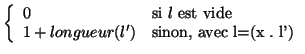 |
(define longueur
(lambda (L)
(if (null? L)
0
(+ 1 (longueur (cdr L)) ) )))
Ex :
Renversement d'une liste : (a b c) -> (c b a)
- 1.
- variable d'induction : la liste
- 2.
- condition d'arrêt : liste vide
résultat : renversement d'une liste vide = liste vide
- 3.
- pour renverser une liste l, si on sait renverser son reste, il suffit d'ajouter le premier élément à la fin du renversement du reste
- 4.
- on fait tendre le problème vers la liste vide en appelant récursivement la fonction sur le reste de l
(define renverse
(lambda (l)
(if (null? l)
'()
(append (renverse (cdr l))
(list (car l))) )))
- 1.
- Vérifier qu'on a un critère d'arrêt et qu'on renvoie la bonne solution pour la taille minimale du problème
- 2.
- Vérifier qu'on fait bien tendre le problème vers la solution triviale, i.e. qu'on atteindra bien le critère d'arrêt
- 3.
- Vérifier la cohérence du nombre d'arguments et du type des expressions lors de l'appel récursif


Next: Notion de complexité
Up: No Title
Previous: Les listes
Regis Girard
2000-02-23