Les listes

7. Paires pointées et listes

Les structures de données les plus utilisées en LISP (et en Scheme) sont les paires pointées et les listes.

7.1 le Type Paire

Une paire pointée correspond à la notion de couple. Si on veut par exemple représenter en Scheme un couple de données composé du nom et de l'âge d'une personne on pourra utiliser une paire pointée dont le premier élément est un symbole ou une chaîne qui représente le nom et le second élément un nombre qui représente l'âge.

Le type Paire est défini par l'ensemble des couples d'objets quelconques, les opérateurs permettant de manipuler des paires sont :

• l'opérateur de construction, cons : Objet, Objet $\longmapsto$ Paire, qui prend en argument deux objets quelconques et renvoie la paire correspondante;
• l'opérateur d'accès au premier élément, car : Paire $\longmapsto$ Objet;
• l'opérateur d'accès au deuxième élément, cdr : Paire $\longmapsto$ Objet;
• le prédicat de type, pair? : Objet $\longmapsto$ Booléen, qui renvoie vrai (#t), si l'objet qu'on lui donne en argument est de type Paire.

La représentation d'une paire pointée en Scheme est la suivante :

Attention : le point qui sépare les deux éléments est très important et il doit être précédé et suivi d'un espace. Ce point permet notamment de faire la différence entre une paire pointée et une liste de deux éléments.

Ex :

   : (cons "florence" 23)        : (cons (+ 12 3) (* 4 5))      : (cons (sqrt 25) (> 2 3))
   ("florence" . 23)             (15 . 20)                      (5 . #f)

   : (car (cons 12 20))          : (cdr (cons (* 2 3) "toto")) 
   12                            "toto"

   : (cdr (cons 12 20))          : (car (cons (cons 1 2) 3))
   20                            (1 . 2)

7.2 Le type Liste

Une liste est une collection ordonnée d'objets quelconques en nombre fini. À la différence d'un ensemble, un objet peut apparaître plusieurs fois dans un même liste et l'ordre est important.

Par exemple la liste constituée des objets 1, 2 et 3 dans cet ordre est différente de la liste des objets 3, 1 et 2 et la liste des objet 3, 3 et 3 est différente de la liste contenant le seul objet 3.

La plus petite liste est celle qui ne contient aucun objet, on l'appelle la liste vide.

Pour noter une liste en Scheme, on écrit ses éléments entre parenthèse en les séparant par des espaces, c'est à dire sous la forme :

Le type Liste est constitué de l'ensemble des listes finies d'objets quelconques auquel on ajoute la liste vide, notée (). On note Liste* l'ensemble des listes non vides. Les opérateurs sur les listes sont les suivants :

• l'opérateur de construction, cons : Objet, Liste $\longmapsto$ Liste, qui prend en argument un objet quelconque o et une liste l et renvoie la liste obtenue en ajoutant l'objet o au début de la liste l;
• l'opérateur d'accès au premier élément, car : Liste* $\longmapsto$ Objet, qui prend en argument une liste non vide et renvoie son premier élément;
• l'opérateur cdr : Liste* $\longmapsto$ Liste, qui prend en argument une liste non vide et qui renvoie le reste de cette liste, c'est à dire la liste sans son premier élément;
• le prédicat null? :Objet $\longmapsto$ Booléen, qui renvoie vrai si son argument est la liste vide;
• le prédicat de type, list? : Objet $\longmapsto$ Booléen, qui renvoie vrai si l'objet qu'on lui donne en argument est une liste.

7.3 Liens entre les paires pointées et les listes

Toute liste non vide peut être obtenue en ajoutant un élément au début d'une autre liste. On peut donc construire n'importe quelle liste à partir de la liste vide.

Ainsi une liste contenant un seul élément est une paire pointée dont le second élément est la liste vide. Par exemple la liste (12) est égale à la paire pointée ( 12 . () ) que l'on obtient en évaluant l'expression (cons 12 '()).

Pour construire la liste (1 2), on procède en raisonnant de la manière suivante : c'est une paire pointée dont le premier élément est le nombre 1 et dont le second élément est la liste (2), c'est à dire une paire pointée dont le premier élément est le nombre 2 et le second la liste vide. On évalue donc l'expression : (cons 1 (cons 2 '())) qui construit la paire pointé (1 . (2 . ())) qui est bien une liste puisque sont deuxième élément (2 . ()) est une liste.

Comme il est fastidieux d'écrire une liste sous la forme (e1 . (e2 . (e3 . ()))), Scheme permet une écriture plus lisible grâce aux règles suivantes :

(X . ()) s'écrit plus simplement (X)

et (X . (Y)) s'écrit (X Y)

La fonction cons rend son résultat sous forme simplifiée.

Ex :

   > (define maliste (cons 1 (cons 2 (cons 3 '()))))        > (car maliste)
   maliste                                                  1
   > maliste                                                > (cdr maliste)
   (1 2 3)                                                  (2 3)

Attention : toute les listes sont des paires pointées mais la réciproque est fausse.

   > (list? maliste)                                   > (pair? maliste)
   #t                                                  #t
   > (list? '())                                       > (pair? '())
   #t                                                  #f
   > (list? (cons 1 2))                                > (pair? (cons 1 2))
   #f                                                  #t

On a les deux axiomes suivants liant les fonctions cons, car et cdr :

Comme on imbrique souvent des car et des cdr, leurs combinaisons jusqu'au quatrième niveau sont prédéfinies. Ainsi, on pourra écrire (cadadr l) à la place de (car (cadr (car (cdr l))))

7.4 Représentation graphique des listes :

On peut s'aider d'un représentation graphique des paires pointées et des listes.

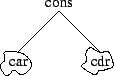
On représente une paire pointée par l'arbre :

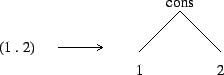
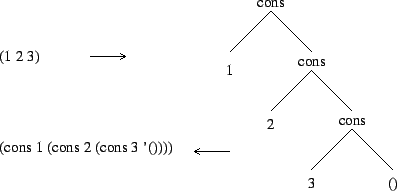
Cette représentation peut être très utile au début pour construire et accéder aux éléments d'une liste.

Par exemple, la liste ( (1 3) 4 (5 6) ) dont le premier élément est (1 3) et le reste (4 (5 6)) peut se représenter par l'arbre suivant :

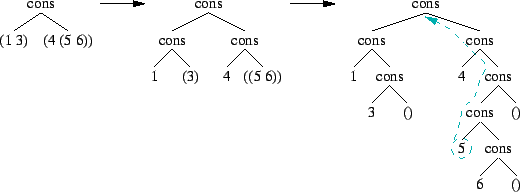
Une fois l'arbre complètement dessiné, on peut facilement trouver l'expressions Scheme qui permet de le construire : (cons (cons 1 (cons 3 '())) (cons (cons 4 '()) (cons (cons 5 (cons 6 '())) '()))).

Si maintenant on veut accéder à un élément donné de la liste, il suffit de le repérer dans l'arbre et de savoir que remonter de la droite correspond à l'opérateur cdr et remonter de la gauche à l'opérateur car. Ainsi pour obtenir le nombre 5 à partir de la liste ((1 3) 4 (5 6)), il faut évaluer l'expression

(car (car (cdr (cdr '((1 3) 4 (5 6))))).