Next: Les listes Up: No Title Previous: Syntaxe et expressions

Sous-sections

Fonctions - Environnements

4. Les fonctions

Scheme est un langage fonctionnel, programmer en Scheme, c'est donc écrire des fonctions, les composer et les évaluer afin de résoudre un problème.

4.1 Notion de type

Un programme informatique prend des données en entrée et calcule un résultat. Toutes les données ne sont pas de même nature. Il y a des données numériques, des symboles, des chaînes de caractères, etc ... On dit qu'il y a différents types de données.

De même qu'ajouter des oranges et des éléphants pour calculer le prix d'une voiture est incohérent, il est tout aussi incohérent d'appliquer la fonction racine carrée à une chaîne de caractère.

La notion de type est essentielle pour utiliser et écrire des fonctions : une fonction ne peut être correctement évaluer que si le nombre et le type des arguments qu'on lui donne correspondent exactement à la définition de cette fonction.

$\fbox{\begin{minipage}{12cm} Un type est d\'efini par un ensemble de valeurs et ... ...diquer qu'un objet $o$\space est de type $T$ , on notera $o\in T$\end{minipage}}$

4.1.1 Le type Booléen

L'ensemble Booléen contient deux valeurs : vrai et faux. En scheme on note la valeur vrai #t (de l'anglais true) et la valeur faux #f (de l'anglais false).

Les opérateurs qui s'appliquent aux booléens sont les opérateurs logiques : et, ou, non qu'on note respectivement and, or et not en scheme.

4.1.2 Le type Entier

Le type Entier est défini par l'ensemble des entiers relatifs, les opérateurs arithmétiques +, -, *, quotient (pour la division entière), remainder (le reste de la division entière) et les comparateurs =, <.

En scheme, contrairement à beaucoup de langage informatique, la taille des entiers n'est pas limitée.

4.1.3 Le type Rationnel

Le type Rationnel est défini par l'ensemble des rationnels, c'est à dire les nombres qui s'écrivent sous la forme p/q avec p et q qui sont des entiers. Les opérateurs sur les rationnels sont +, -, *, / et les comparateurs = et <.

Un nombre rationnel s'écrit en scheme sous la forme p/q. Tous les calculs sur les rationnels sont des calculs exacts, l'interprète ne renvoie pas de valeur approchée.

4.1.4 Le type Réel

Contrairement aux entiers et aux rationnels, le type Réel ne correspond pas à l'ensemble $\mathbb R$ des mathématiques. Aucun nombre de $\mathbb R$ dont l'écriture décimale est infinie n'appartient au type Réel, tout simplement parce qu'on ne peut pas le représenter en machine.

À cause de ce problème de représentation, les calculs sur les nombres réels ne sont pas exacts et peuvent être entachés d'erreur. Pour la même raison, bien que l'opérateur d'égalité puisse être utilisé avec des réels, il n'a aucune signification et peut renvoyer un résultat faux.

Un réel s'écrit sous forme décimal en utilisant le point comme séparateur décimal. On peut aussi les écrire avec la notation scientifique. Par exemple 123.4567, 1.234567e2, -6.65e-23 sont des réels.

4.1.5 Le type Chaîne

Le type Chaîne contient toutes les chaînes de caractères. Les opérateurs sont :

: la longueur (string-length) qui renvoie le nombre de caractères d'une chaîne;
: la concaténation (string-append) qui construit une nouvelle chaîne en en mettant deux bout à bout;
: le test d'égalité (string=?) qui rend vrai si deux chaînes sont égales, c'est à dire si elles sont formées des mêmes caractères dans le même ordre.

On représente une chaîne par la suite des caractères qui la composent encadrée par des guillemets. La plus petite chaîne est la chaîne vide : "".

   > (string-length "toto x 23")            >(string-append "toto" "titi tutu")
   9                                        "tototiti tutu"

4.2 Spécification d'une fonction

Une fonction est définie par le nombre et le type des données qu'elle prend en entrée et un algorithme qui permet de calculer le résultat à partir des données.

Une fonction peut avoir 0 ou plusieurs paramètres ou arguments en entrée mais elle ne fournit qu'un seul résultat.

Donner la spécification d'une fonction, c'est donner son profil, c'est à dire le type et l'ordre de ses paramètres et le type de son résultat, ainsi que ses paramètres formels et une description du résultat.

$\fbox{ \begin{tabular}{ccc} Types des param\\lq etres & $\longrightarrow$\space & T... ...\\lq etres formels & $\longmapsto$\space & Description du r\'esultat \end{tabular}}$

Par exemple :

Réel	$\longrightarrow$	Réel
x	$\longmapsto$	le carré de x

Les noms des paramètres formels sont donnés ``pour la forme'', la fonction précédente reste la même si on appelle le paramètre formel y ou toto ou zero. L'important est de lui donner un nom pour pouvoir y faire référence dans la description du résultat.

Un autre exemple, une fonction d'arité 2 :

Réel, Entier₊	$\longrightarrow$	Réel
x, a	$\longmapsto$	x élevé à la puissance a

4.3 Représentation d'une fonction

La représentation d'une fonction en Scheme se fait à l'aide d'une expression composée qu'on appelle lambda-expression dont la forme est la suivante :

$\fbox{\bf (lambda (arg$_1$\space arg$_2$\space \ldots arg$_n$ ) $<$ expression$>$ ) }$

où

arg₁ arg₂ ...arg_n sont des symboles qui représentent les paramètres formels de la fonction
<expression> est une expression qu'on appelle corps de la lambda-expression et qui code la manière de calculer le résultat de la fonction.

Par exemple, on peut représenter la fonction :

Réel $\longrightarrow$ Réel

x $\longmapsto$ le carré de x

par la lambda-expression
(lambda (x) (* x x)) ou bien (lambda (truc) (* truc truc)).

La valeur de cette expression est une fonction, on utilise donc cette lambda-expression comme n'importe quelle autre fonction prédéfinie.

: > ( (lambda (x) (* x x)) 5 )
25
: > ( (lambda (x) (* x x)) (+ 7 3) )
100
: > ( (lambda (x) (* x x)) (sqrt 2) )
2

4.4 Évaluation de l'appel d'une lambda-expression

L'évaluation d'une expression composée de la forme ( (lambda (arg₁ ...arg_n) <expr>) a₁ ...a_n ) se fait de la manière suivante :

1.: l'interprète évalue chacun des arguments a₁ ...a_n dans un ordre non déterminé a priori;
2.: il évalue la lambda-expression dont la valeur est une fonction;
3.: il crée temporairement les associations entre chaque paramètre formel et le paramètre effectif correspondant, c'est à dire qu'il associe au paramètre formel arg₁ la valeur de a₁ etc ...;
4.: il évalue l'expression composée formée par le corps de la lambda-expression.

Par exemple, l'évaluation de l'appel ( (lambda (x y) (* x y)) (+ 7 3) 5) peut se dérouler ainsi :

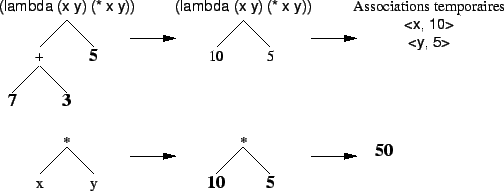
$\includegraphics{./evallambda.eps}$

4.5 Nomage d'une lambda-expression

Afin de ne pas avoir à écrire plusieurs fois la même lambda-expression lorsqu'on a besoin de faire de multiples appels à une fonction donnée, Scheme permet d'associer un symbole à une lambda-expression en utilisant la même fonction prédéfinie define déjà vue pour définir des variables. On parle alors de variable fonctionnelle.

$\fbox{\bf (define $<$ identificateur$>$\space $<$ lambda-expression$>$ )}$

Ainsi, on peut définir une variable fonctionnelle carre (par abus de langage on dira la fonction carre) dont la valeur est la fonction spécifiée par

Réel $\longrightarrow$ Réel

x $\longmapsto$ x²

et l'utiliser comme n'importe qu'elle autre fonction prédéfinie.

          > (define carre (lambda (x) (* x x)) )
          carre
          > (carre 12)
          144

5. Définition, évaluation et environnement

L'évaluation d'une expression nécessite de trouver les valeurs associées aux différents symboles qui apparaissent dans celle-ci. Le mécanisme d'évaluation est donc lié à la recherche de ces valeurs. L'espace dans lequel s'effectue cette recherche est appelé environnement.

ENVIRONNEMENT GLOBAL : c'est l'environnement qui se situe au plus haut niveau de l'interprète Scheme, c'est dans cet environnement que sont définis les symboles auxquels sont associées les fonctions prédéfinies.

Lorsqu'on définit une variable, cela revient à ajouter dans l'environnement courant un symbole auquel on associe une valeur.

Lorsqu'on évalue un symbole, cela revient à rechercher dans l'environnement courant si ce symbole est défini et a rendre la valeur qui lui est associé.

ENVIRONNEMENT LOCAL : en opposition à l'environnement global, on distingue l'environnement local qui est un ensemble de liaisons temporaires entre des identificateurs et des valeurs. Ces liaisons n'existent que le temps d'évaluer l'expression pour laquelle elles sont créées.

5.1 Définition d'un environnement local

Définir un un environnement local se fait à l'aide de la forme spéciale let :

$\fbox{\bf (let ( ($<$ ident$_1>$\space $<$ expr$_1>$ ) ($<$ ident$_2>$\space $<$ expr$_2>$ ) \ldots ) $<$ corps$>$\space )}$

Cette forme a pour effet de définir les liaisons <ident₁, valeur de expr₁ >, <ident₂, valeur de expr₂ > ...créant ainsi un environnement local dans lequel l'expression <corps> est évaluée.

On peut traduire cela par : ``posons ident₁ vaut expr₁, ident₂ vaut expr₂, etc ...et calculons la valeur de corps''.

Pourquoi définir un environnement local ?

pour ne pas polluer l'environnement global
pour éviter d'évaluer plusieurs fois une même expression lors d'un calcul

5.2 Évaluation d'un let

Une expression let s'évalue de la manière suivante :

toutes les expressions expr_i sont évaluées dans l'environnement courant Env;
les liaisons locales <ident_i, valeur de expr_i > sont ajoutées à l'environnement Env pour donner un environnement locale Env';
l'expression corps est évaluée dans Env' et le résultat est retourné;
les liaisons locales sont détruites et l'environnement redevient Env.

On peut ainsi définir une successions d'environnements imbriqués les uns dans les autres. Lorsque l'interprète doit évaluer un symbole, il va d'abord chercher la valeur de ce symbole dans l'environnement courant. Si ce symbole y est défini il rend sa valeur, sinon il ira successivement chercher dans les niveaux supérieurs. S'il atteint le niveau le plus haut de l'interprète et que le symbole n'y est pas défini, alors il rend une erreur.

Ex :

     > (define carre 
           (lambda (x) (* x x)))
     carre
     > (define aire-disque
           (lambda (r)
              (let ( (pi 3.1416) )
                   (* pi (carre r)) )))
     aire-disque
     > (define r1 10)
     r1
     > (aire-disque r1)
     98.6965056
     > (carre r)
     erreur
     > pi
     erreur

; Définition de la fonction carre : Réel $\rightarrow$ Réel,
; x $\longmapsto$ x²

; Définition de la fonction aire-disque : Réel $\rightarrow$ Réel,
; r $\longmapsto$ $\pi.r^2$
Création d'un environnement local contenant < pi, 3.1416 >

; Définition de la variable r1 dans l'environnement global

; Évaluation de (aire-disque r1)
; L'interprète trouve la valeur de r1 et évalue l'expression

; r n'est pas défini dans l'environnement global
; pi est une variable définie dans l'environnement
; local à la fonction aire-disque

5.3 La forme spéciale let*

Lors de l'évaluation d'un let, l'interprète évalue d'abord toutes les expressions avant de créer les liaisons dans l'environnement local. Comment faire si l'on désire définir une variable locale en fonction d'une autre ?

Par exemple si on veut une environnement dans lequel ``on pose : a vaut 2, b vaut 5*a et c vaut b-a'', on est obligé décrire :

    (let ( (a 2 ))
       (let ( (b (* 5 a)) )
          (let ( (c (- b a)) )
              ;; ici a vaut 2, b vaut 10 et et c vaut 8
              ;; un calcul
          )
       )
     )

Heureusement il existe une manière plus concise de l'écrire a l'aide de la forme spéciale let* dont la syntaxe est :

$\fbox{\bf (let* ( (ident$_1$\space expr$_1$ ) (ident$_2$\space expr$_2$ ) \ldots ) corps )}$

Contrairement au let, lors de l'évaluation de la forme spéciale let* l'environnement local est modifié en créant successivement les liaisons <ident_i, valeur de expr_i > dans l'ordre d'écriture.

L'expression expr₁ est évaluée dans l'environnement courant et sa valeur est liée au symbole ident₁, puis expr₂ est évaluée dans l'environnement courant auquel a été ajouté la liaison <ident₁, valeur de expr₁ > et ainsi de suite pour toutes les variables temporaires définies. Ensuite, le corps du let* est évalué dans l'environnement résultant de l'environnement initial et de toutes les nouvelles liaisons.

     (let* ( (a 2) (b (* 5 a)) (c (- b a)) )
          ;; ici a vaut 2, b vaut 10 et et c vaut 8
          ;; un calcul 
     )

5.4 Définition locale de fonction

Il arrive, pour décomposer un calcul, qu'on ait besoin d'une fonction particulière mais de manière temporaire, juste le temps du calcul. On peut alors définir cette fonction localement. Il suffit pour cela de placer sa définition à l'intérieur d'une fonction principale.

      (define fonctionprincipale
         (lambda ( ... )
             (define fonctionlocale
                 (lambda ( ...) 
                 ;; corps de la fonction locale
                 ))
             ;; corps de la fonction principale
             ;; dans lequel on peut utiliser la fonction locale
         ))

De cette manière, fonctionlocale n'existe qu'à l'intérieur de fonctionprincipale dans l'environnement locale à la fonction principale.

6. Structures de contrôle conditionnelles

Pour pouvoir programmer des fonctions un peu complexes, il est nécessaire de pouvoir faire des tests et de disposer d'expressions conditionnelles afin de faire des choix dans le déroulement d'un programme.

6.1 Prédicats

Un prédicat est une fonction -prédéfinie ou définie par le programmeur- qui rend une valeur booléenne. Souvent, et par convention, les symboles représentant des prédicats se terminent par une point d'interrogation.

Voici quelques prédicats prédéfinis :

$\bullet$

=, <, >, <= ,>=, even?, odd? permettent de comparer des nombres ou des expressions dont les valeurs sont des nombres. even? rend vrai pour un nombre pair et odd? rend vrai pour un nombre impair.

Ex :

   > (< 2 3)                             > (odd? 15)
   #t                                    #t
   > (>= (+ 1 3) 12)                     > (= (* 3 2) (/ 24 4))
   #f                                    #t

$\bullet$

le prédicat zero? rend vrai si la valeur de l'expression à laquelle on l'applique est 0.

$\bullet$

le prédicat equal? prend en argument deux expressions et rend vrai si leurs valeurs sont égales.

Ex :

   > (equal? "toto" "toto")            > (equal? 12 (* 6 2))
   #t                                    #t

6.2 Opérateurs booléens

L'opérateur logique de négation est la fonction not : (not #f) rend #t et (not #t) rend #f. Aux opérateurs logiques et et ou correspondent les fonctions booléennes and et or. Attention, ce sont des formes spéciales, c'est à dire qu'elles n'évaluent leurs arguments que si cela est nécessaire. Contrairement aux autres expressions composées les arguments sont évalués dans l'ordre de leur apparition.

Ex :

     : (and #f #t)
     #f
     : (or (= 2 2) (= 3 (/ 5 0)))       
     #t                                      ; sans faire d'erreur
     : (and (> 4 12) (= 3 (/ 5 0)))
     #t                                      ; sans faire d'erreur
     : (or (> 4 12) (= 3 (/ 5 0)))
     erreur

Pour évaluer (or (= 2 2) (= 3 (/ 5 0))) l'interprète évalue d'abord l'expression (= 2 2) et comme celle-ci rend vrai, l'évaluation est terminée, ce qui explique qu'il n'y a pas d'erreur.

Pour évaluer (or (> 4 12) (= 3 (/ 5 0))) l'interprète évalue d'abord l'expression (> 4 12); celle-ci rendant faux, il est nécessaire d'évaluer l'expression (= 3 (/ 5 0)) qui provoque une erreur.

6.3 Expressions conditionnelles

6.3.1 Le if

La forme spéciale if permet d'évaluer une expression de choix :

$\fbox{\bf (if $<$ test$>$\space $<$ expr1$>$\space $<$ expr2$>$ )}$

L'évaluation de la fonction if se fait de la manière suivante :
on évalue l'expression <test>
si sa valeur est vraie, if rend la valeur de <expr1>
sinon, if rend la valeur de <expr2>

Attention, if est aussi une forme spéciale, les expressions <expr1> et <expr2> ne sont évaluées que si c'est nécessaire et de toute façon jamais toutes les deux.

Ex : la fonction valeur absolue dont la spécification est la suivante :

absolue :	Réel	$\longrightarrow$	Réel₊
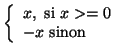	x	$\longmapsto$	$\left\{\begin{array}{l} x, \mbox{ si } x>=0\\ -x \mbox{ sinon} \end{array}\right.$

peut se définir en Scheme par :

(define absolue 
   (lambda (x)
      (if (>= x 0)
           x
          (- x))))

6.3.2 Le cond, expression conditionnelle multiple

Le cond est une généralisation du if. Sa syntaxe est la suivante :

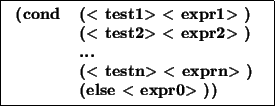
$\fbox{\bf \begin{tabular}{ll} (cond & ($<$ test1$>$\space $<$ expr1$>$ )\\ & (... ...& ($<$ testn$>$\space $<$ exprn$>$ )\\ & (else $<$ expr0$>$ )) \end{tabular} }$

C'est également une forme spéciale dont le mécanisme d'évaluation est le suivant :

: <test1> est évalué dans l'environnement courant et si sa valeur est vraie, cond rend la valeur de <expr1>
: sinon, <test2> est évalué et si sa valeur est vraie, cond rend la valeur de <expr2>
: etc ...
: si aucun des <testi> n'est vrai alors cond rend la valeur de <expr0>

Attention : on peut écrire une expression cond sans clause else, dans ce cas, si aucun des tests ne rend vrai la valeur l'évaluation rendra la valeur #[undefined]

Ex : la fonction truc dont la spécification est la suivante :

truc :	Réel	$\longrightarrow$	Réel₊
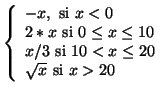	x	$\longmapsto$	$\left\{\begin{array}{l} -x, \mbox{ si } x<0\\ 2*x \mbox{ si } 0\leq x \leq 10\\ x/3 \mbox{ si } 10<x\leq 20\\ \sqrt x \mbox{ si } x>20 \end{array}\right.$

peut se définir en Scheme par :

(define truc 
   (lambda (x)
      (cond ((< x 0) (- x))
            ((<= x 10) (* 2 x))
            ((<= x 20) (/ x 3))
            (else (sqrt x)))))

Et si le cond n'existait pas ...

(define truc 
   (lambda (x)
      (if (< x 0) 
          (- x)
          (if (<= x 10) 
              (* 2 x)
              (if (<= x 20) 
                  (/ x 3)
                  (sqrt x))))))

Next: Les listes Up: No Title Previous: Syntaxe et expressions

Regis Girard
2000-02-23