Syntaxe et expressions

1. Expressions

Dans le langage courant, par exemple en français, on exprime une idée à l'aide d'une phrase ou d'une expression. Une phrase est construite à partir de mots, eux même construits à partir des lettres de l'alphabet. Pour bien se comprendre on ne construit pas ces phrases n'importe comment, on suit un ensemble de règles qu'on appelle la syntaxe ou la grammaire.

Dans un langage informatique, il en va de même : pour ``dialoguer'' avec un ordinateur on forme des expressions à partir de mots (qu'on appelle aussi symboles ou expressions atomiques) construits à partir d'un alphabet. Et pour être ``interprétées'' par l'ordinateur ces expressions doivent suivre une syntaxe rigoureuse.

Différentes représentations d'une expressions

Exemples d'expressions du langages des mathématiques :

12*(3+10) $\sqrt{3*x+2}$ $\ln(x+1)/\sin(x)$

Représentation sous forme d'arbre :

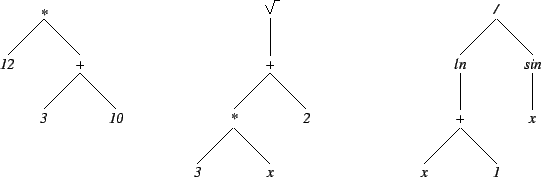
Écriture préfixée : on écrit le symbole d'une fonction devant ses arguments.

$*\ 12\ +\ 3\ 10$ $\sqrt{}\ +\ *\ 3\ x\ 2$ $/\ \ln\ +\ x\ 1\ \sin\ x$

Écriture postfixée : on écrit le symbole d'une fonction après ses arguments.

$12\ 3\ 10\ +\ *$ $3\ x\ *\ 2\ +\ \sqrt{}$ $x\ 1\ +\ \ln\ x\ \sin\ /$

L'écriture usuelle des expressions mathématiques combine l'écriture préfixée pour la plupart des fonctions (par exemple $\sin(x+1)$, l'écriture postfixée pour certaines fonctions (par exemple x², n!), et l'écriture infixée pour les opérateurs (+, -, *, /).

2. La syntaxe de Scheme

La syntaxe de Scheme est très simple et permet d'aborder la programmation très rapidement.

Scheme est un langage interprété. L'interprète évalue au fur et à mesure les expressions que le programmeur écrit.

Nous appelons expression tout ce que nous manipulons en Scheme, c'est à dire tous ce qu'on demande d'évaluer à l'interprète ainsi que tous les résultats que renvoie ce dernier.

Il existe deux types d'expressions en Scheme : les expressions atomiques et les expressions composées.

2.1 Les expressions atomiques

Les nombres : entiers, réels, rationnelles, complexes.

Les booléens : ils s'écrivent #t pour vrai et #f pour faux.

Les chaînes de caractères : elles commencent et finissent par des double-quotes ".

Ex : "toto", "une autre chaine"

Les symboles : ce sont des noms contenant des lettres, des chiffres ou des signes comme +, -, !, ?, _, mais pas d'espace.

Ex : toto, a12, to+to

2.2 Les expressions composées

Pour écrire des expressions composées en Scheme, on utilise l'écriture préfixée. Une expressions Scheme est donc de la forme :

où fonc est une fonction d'arité n (c'est à dire qui prend n paramètres en entrée) et arg_1 arg_2 ...arg_n sont les n arguments de cette fonction. Ex :

        (+ 34 67)               (/ 567 45)            (- 12)            (cos 3.1416)

On peut voir une expression composée Scheme comme un appel de fonction.
Un appel de fonction doit toujours contenir autant d'arguments que l'arité de la fonction.
Les arguments d'une fonction peuvent être des expressions composées.

La notation préfixée autorise :

-

une extension aisée aux fonctions (ou procédures) qui admettent un nombre variable d'arguments :

     (+ 12 3 56 7 20)

-

l'imbrication des expressions. Par exemple, l'expression 2 * 3 + 12 - 6 s'écrit (+ (* 3 5) (- 12 6))

Cependant l'écriture préfixée n'est pas toujours très lisible :

     (+ (* 3 (+ (* 2 4)(+ 3 5)))(+ (- 10 7) 6))

c'est pourquoi on attachera un soin tout particulier à indenter les expressions :

     (+ (* 3
           (+ (* 2 4)
              (* 3 5)))
        (+ (- 10 7)
           6))

3. Évaluation des expressions

L'interprète Scheme fonctionne selon le cycle suivant :

Nous allons voir comment Scheme évalue chaque type d'expression, c'est à dire comment l'interprète calcule la valeur d'une expression.

3.1 Les constantes

Les constantes sont les nombres, les booléens et les chaînes de caractères. L'évaluation d'une constante par l'interprète Scheme renvoie la constante elle-même.

Ex :

     > 12.345                  > #t                  > "une chaine"
     12.345                     #t                   "une chaine"

3.2 Les symboles

3.2.1 Définition de variables

Comme dans la plupart des langages de programmation, il est pratique de pouvoir définir des variables.

Définir une variable, c'est créer un lien, une association, entre un identificateur et une valeur. En Scheme, cette opération se fait par l'intermédiaire de la fonction prédéfinie define :

qui a pour effet de créer un lien entre un identificateur qui est un symbole et la valeur retournée par l'évaluation de l'expression.

Ex :

     > (define pi 3.1416)                           > (define deux (+ 1 1))
     pi                                             deux
     > pi                                           > (* deux pi)
     3.1416                                         6.2832

3.2.2 Évaluation

L'évaluation d'un symbole consiste simplement à rendre la valeur qui lui est associé. Par exemple, l'évaluation du symbole pi rend 3.1416 car c'est la valeur qui lui a été associée lors de sa définition.

Si la variable que l'on veut évaluer n'existe pas, c'est à dire si on ne l'a pas défini au préalable une association entre le symbole représentant la variable et une valeur, alors l'interprète renvoie une erreur.

3.3 Les expressions composées

L'évaluation d'une expression composée, de la forme : (f a1 a2 ... an) se fait en deux étapes :

1.

l'interprète évalue chacun des arguments a1 ... an dans un ordre non déterminé a priori

2.

il applique la fonction f aux valeurs des arguments et rend le résultat.

Bien entendu pour que cette évaluation se fasse sans erreur il faut que la fonction f existe et que le nombre d'arguments soit égal à son arité.

Ex : Pour évaluer l'expression (* 2 3), l'interprète évalue d'abord les nombres 2 et 3 dont les évaluations sont 2 et 3, puis leur applique la fonction prédéfinie + et rend 7.

Ex : Pour évaluer (+ (* 2 5) (* 3 4)), l'interprète évalue d'abord les expressions (* 2 5) et (* 3 4) dont les résultats sont 10 et 12, puis il évalue l'expression (+ 10 12) et rend 22.

3.4 Blocage de l'évaluation

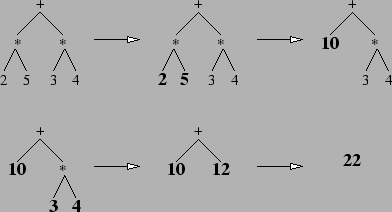
L'interprète de Scheme évalue toute les expressions qu'on lui soumet. Or parfois, on aimerait pouvoir manipuler une expression et non pas sa valeur. On peut bloquer le mécanisme dévaluation en appliquant à une expression la fonction spéciale quote. Cette fonction se contente de renvoyer son argument sans l'évaluer. On dit alors que l'expression est ``quotée''.

Ex :

     >pi                       > (quote pi)
     3.1415                    pi

Cette fonction est si souvent utilisée qu'il existe une notation abrégée : le caractère apostrophe qu'on appelle aussi le quote. Lors de l'évaluation, l'interprète remplace l'apostrophe par la fonction quote. Ainsi on aura :

     > (+ 1 2)                 >(quote (+ 1 2))                 >'(+ 1 2)
     3                         (+ 1 2)                          (+ 1 2)

     > toto                    >'toto                           >''toto 
     erreur                    toto                             'toto

Il est inutile (mais cela ne produit pas d'erreur) de ``quoter'' une constante, c'est à dire : un nombre, un booléen ou une chaîne.