Programmation d'ordre supérieur

Les langages de programmation fonctionnelle et Scheme en particulier permettent de faire de la programmation d'ordre supérieure. Cela consiste à manipuler des fonctions comme on manipule d'autres types de données. C'est à dire qu'une fonction peut avoir des fonctions comme arguments et comme résultat. Cette caractéristique permet entre autre de faire de l'abstraction de fonctions.

15. Des fonctions en arguments

15.1 Exemples

Écrivons une fonction qui multiplie par deux chaque élément d'une liste de nombres :

      (define fois2
         (lambda (l)
            (if (null? l)
                '()
                (cons (* 2 (car l)) (fois2 (cdr l))))))

Si maintenant on veut une fonction qui calcule la racine carrée de chaque élément, on écrit :

      (define racine-tous
         (lambda (l)
            (if (null? l)
                '()
                (cons (sqrt (car l)) (racine-tous (cdr l))))))

En observant ces deux fonctions, on voit qu'elles ont le même schéma :

      (define NOMFONC
         (lambda (l)
            (if (null? l)
                '()
                (cons (FONCTION (car l)) (NOMFONC (cdr l))))))

15.2 Abstraction

Maintenant, si l'on veut une fonction qui élève au carré chaque élément, ou bien qui prend l'inverse de chaque élément, il faut à chaque fois écrire une fonction différente mais dont le schéma est le même.

La programmation d'ordre supérieure nous permet de définir une fonction qui applique une fonction à chaque élément d'une liste. On conserve le schéma général des deux fonctions précédentes et on ajoute un paramètre supplémentaire qui correspond à la fonction que l'on veut appliquer à chaque élément de la liste :

      (define applique-a-tous 
         (lambda (f l)
             (if (null? l)
                 '()
                 (cons (f (car l)) (applique-a-tous f (cdr l))))))

La fonction applique-a-tous est une abstraction des fonctions fois2, racine-tous, ...On peut récrire ces fonctions de la manière suivante :

      (define fois2 
         (lambda (l) 
             (applique-a-tous (lambda (x) (* 2 x)) l)))

      (define racine-tous
         (lambda (l)
            (applique-a-tous sqr l)))

Et si on veut calculer le cube de chacun des éléments on écrit :

      (define tous-au-cube
         (lambda (l)
            (applique-a-tous (lambda (x) (* x x x))  l)))

15.3 La fonction map

La fonction applique-a-tous est tellement utile qu'elle est prédéfinie en Scheme. Elle s'appelle map et constitue une version plus générale de applique-a-tous car elle peut s'utiliser avec plusieurs listes. Dans ce cas la lambda-expression que l'on passe en argument doit avoir autant de paramètres qu'il y a de listes. Si les listes ont des longueurs différentes, map s'arrête dès que la plus petite liste est vide.

Ex :

      : (map (lambda (x) (+ x 10)) '(1 2 3 4 5))
      (11 12 13 14 15)

      : (map (lambda (x y) (+ x y)) '(1 2 3 4) '(10 20 30 40))
      (11 22 33 44)

      : (map (lambda (a) (cons a '())) '(1 a 2 b))
      ((1)(a)(2)(b))

      : (map (lambda (a b c) (list a b c)) '(1 2 3) '(a b) '(v w x y z))
      ((1 a v)(2 b w))

16. Des fonctions comme résultat

On a vu qu'il est possible de passer des fonctions en tant que paramètres. L'autre aspect de la programmation d'ordre supérieure et de pouvoir définir des fonctions dont le résultat est lui-même une fonction.

Ex 1 : Composition de fonctions

Étant données deux fonctions $f : E_1 \rightarrow E_2$ et $g : E_2 \rightarrow E_3$, on veut construire la fonction composée : $f\circ g : E_1 \rightarrow E_3$. On définit une fonction compose qui prend comme paramètres deux fonctions f et g et rend une fonction.

compose :	Fonction, Fonction	$\longrightarrow$	Fonction
	f, g	$\longmapsto$	$f\circ g$

      (define compose 
         (lambda (f g)
             (lambda (x) (f (g x))) ))

Exemple d'utilisation :

      : (define carre (lambda (x) (* x x)))
      carre
      : (define plus1 (lambda (x) (+ 1 x)))
      plus1
      :(compose carre plus1)
      #[procedure]
      :( (compose carre plus1) 4)
      25

Ex 2 : Puissance nième d'une fonction

Étant donnée une fonction d'arité 1, $f : E \rightarrow E$, on veut construire la puissance nième de f : $f^n=\underbrace{f\circ f\circ \ldots \circ f}_{n}$.

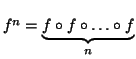On définit une fonction compose-n-fois dont la spécification est :

compose-n-fois :	Fonction, Entier	$\longrightarrow$	Fonction
	f, g	$\longmapsto$	$\left\{ \begin{array}{ll} f & \mbox{ si {\em n=1}}\\ f \circ \mbox{compose-n-fois}(f, n-1) & \mbox{ sinon} \end{array}\right.$

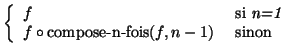      (define compose-n-fois 
         (lambda (f n)
            (if (= n 1)
                f
                (lambda (x) (f ((compose-n-fois f (- n 1)) x))) )))

Ex 3 : Dérivée d'une fonction

Étant donnée une fonction f, on veut construire une fonction qui calcule une approximation de la dérivée de f. Pour dx "petit", on définit la fonction dérivée f' par :

$$f': x \mapsto \frac{f(x+dx) - f(x)}{dx}$$

d'où la fonction Scheme :

      (define derive 
         (lambda (f dx)
             (lambda (x) (/ (- (f (+ x dx)) (f x))
                         dx))))

Exemple d'utilisation :

      : (define cube (lambda (x) (* x x x)))
      cube
      : ( (derive cube 0.0001) 10)
      300.00300000893