L'exécution d'un programme a toujours un coût. Il existe deux paramètres essentiels pour mesurer ce coût :
L'analyse de la complexité consiste à déterminer une fonction associant un coût (en unité de temps ou de mémoire) à chaque entrée soumise à l'algorithme. En fait, on peut se contenter d'associer un coût à un paramètre entier n qui résume la taille de la donnée :
Pour la complexité en temps, il existe une opération répandue : calculer (en fonction de n) le nombre d'opérations élémentaires (addition, comparaison, affectation, ...) requise par l'exécution puis multiplier par le temps moyen de chacune d'elle. Mais problème pour les accès à la mémoire. Il faut donc faire preuve de bon sens !
,
, 
, ...),Quelle complexité ? On distingue, en effet, trois sortes de complexités :
Le type de complexité dépend de l'application (par exemple : réseau téléphonique, commande de freinage, ...).
qui, à un paramètre n dépendant de la donnée soumise à
l'algorithme (en général, n est la taille de cette donnée),
associe le coût f(n) (exprimé en unités arbitraires de temps ou
d'espace) de l'exécution de algorithme pour la donnée.
.
Algorithme proposé :
passe à
vrai, on sort de la boucle et dans tous les cas, i augmente de 1
et i est borné par n.
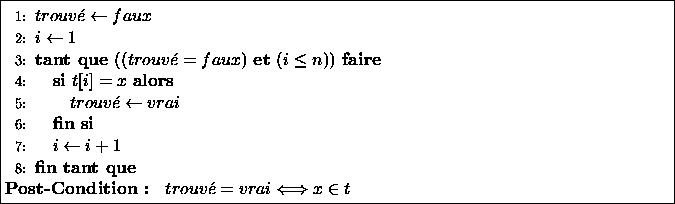
à la fin du programme est vérifiée. Pour cela, montrons que :
est un invariant de la boucle.
. Si au point 3
alors 
et :
alors
si au point 3, 
alors 
et :
alors 
, la
propriété vérifiée au point 5 
devient : 
alors 
alors i > n or i augmente de
1 en 1 donc i = n + 1 et 
.
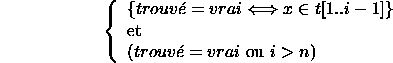
En conclusion, en 8 on a bien :
donc la correction partielle est assurée. Comme nous avons montré la terminaison, l'algorithme est donc correct.
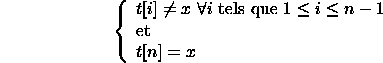
Hypothèse : les éléments de t, ainsi que x, 
Il existe donc 
tableaux distincts. Parmi ceux-ci, il y a
tableaux pour lesquels le coût sera n : les n-1
premiers éléments sont différents de x (le n-ième peut être x ou
différent de x). D'autre part, pour tout 
, il y a
tableaux pour lesquels le coût sera k (les
k-1 premiers éléments diffrérents de x, le k-ième égal à x, les
autres dans [1,p]).
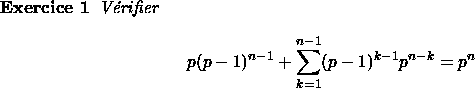
Le coût moyen est donc :
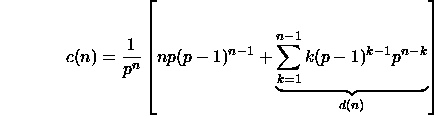
Simplifions cette expression :
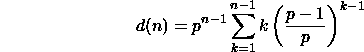
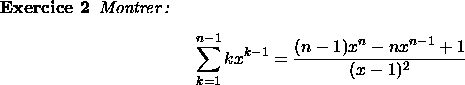
D'où :
et enfin :
Application : on récupère un paquet de 1000 copies d'un partiel noté en point entier de 0 à 20. On se demande s'il y a un étudiant qui a obtenu 20.
Soient f et g deux applications de 
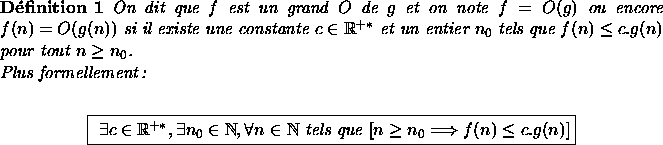
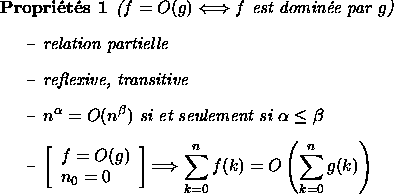
Lors de l'analyse de complexité, on essaie de se ramener aux classes suivantes (données par complexité croissante) :
.
.
.
.
avec k > 1.
.
avec a > 1.
Etude de suites 
telles que :
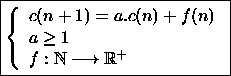
De telles suites interviennent dans l'analyse de complexité d'algorithmes récursifs tels que :
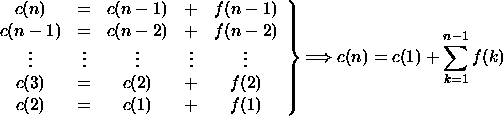
Supposons 
, pour 
; d'après
l'exercice 7,
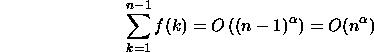
d'où
:
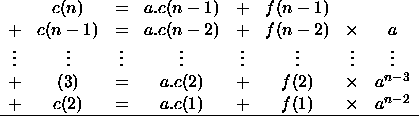
donc
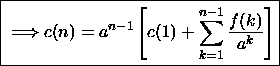
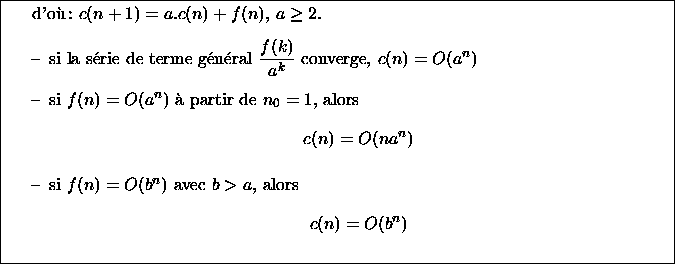
La stratégie ``diviser pour régner'' consiste `a découper la donnée en
deux parts (ou plus) de tailles identiques ( 
), puis à appliquer
l'algorithme une (ou plus) fois à l'une de ces parts, avant de
combiner les résultats pour construire la solution pour la donnée
initiale. D'où, si le partage d'une donnée s'effectue équitablement :
, ce qui nous ramène à :
i.e.
Posons 
; alors 
Par sommation et télescopage :
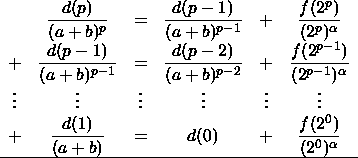
donc
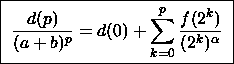
en repassant à la suite (c)
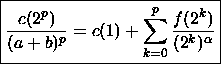
Le comportement asymptotique de c(n) dépend de la nature de la série
de terme général 
.
Examinons les trois cas pour lesquels on peut conclure :
) :
alors :
avec 
alors :
croît pour 
par
récurrence :
car 
. 
et montrons 
; on a :
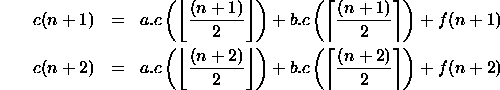
or
donc
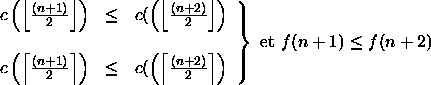
d'où
(où 
).
.
alors :
montre que 
. On aboutit à une conclusion
analogue si 
.
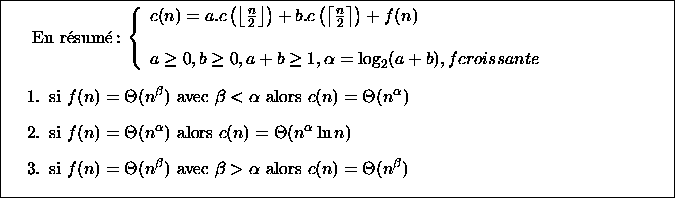
Complexité des algorithmes
This document was generated using the LaTeX2HTML translator Version 96.1 (Feb 5, 1996) Copyright © 1993, 1994, 1995, 1996, Nikos Drakos, Computer Based Learning Unit, University of Leeds.
The command line arguments were:
latex2html -split 0 cours.tex.
The translation was initiated by Jean-Christophe Soulie on mardi, 20 avril 1999, 09:09:14 GMT+4
