Exercices NP-complétude
Exercice 1
- Déterminer la complexité en temps de la MTD M1 (cf. cours p. 189) :
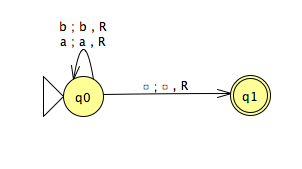
- Déterminer la complexité en temps de la MTND M2 (cf. cours p. 205) :
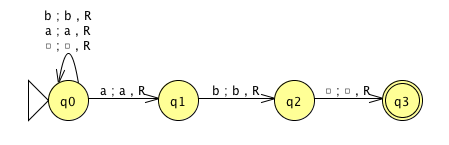
Exercice 2
- Soient L1 et L2 deux langages appartenant à la classe de complexité P.
Quelle est la classe de complexité des langages L1 ∩ L2 et L1 ∪ L2 ?
- Soient L1 et L2 deux langages appartenant à la même classe de complexité NP.
Quelle est la classe de complexité des langages L1 ∩ L2 et L1 ∪ L2 ?
Exercice 3
On rappelle que SAT (décider si une formule booléenne sous forme CNF admet au moins une interprétation la satisfaisant) est NP-complet.
On nomme DOUBLE-SAT le problème de décider si une formule booléenne CNF φ admet au moins deux interprétations
(restreintes aux variables de φ) distinctes la satisfaisant. Par exemple :
- la formule
x ∧ y est une instance négative de DOUBLE-SAT
car il n'y a qu'une interprétation (I(x) = I(y) = 1) qui la satisfait ;
- la formule
x ∧ ¬ x est également une instance négative
car aucune interprétation ne la satisfait ;
- en revanche, la formule
(x ∨ ¬ x) est une instance positive
(I(x)=0 et I(x)=1 satisfont cette formule).
Questions :
- La formule
x ∧ y ∧ (z ∨ ¬ z) est-elle une instance positive ou négative
de DOUBLE-SAT ?
- La formule
x ∧ ¬ x ∧ (z ∨ ¬ z) est-elle une instance positive ou négative
de DOUBLE-SAT ?
- La formule
(x ∨ ¬ x) ∧ (z ∨ ¬ z) est-elle une instance positive ou négative
de DOUBLE-SAT ?
- Pour montrer que DOUBLE-SAT est dans NP, 2 solutions sont possibles :
- proposez un algorithme non-déterministe résolvant DOUBLE-SAT
- argumentez que la validation d'une solution est polynomiale en temps relativement
à la taille de l'instance.
- Montrez que DOUBLE-SAT est NP-complet.
Exercice 4
On précise la démonstration SAT α 3-SAT
en justifiant l'équisatisfiabilité d'une CNF ψ quelconque et
de sa transformée ψ', CNF à 3 littéraux.
Pour chaque cas ci-dessous, montrez :
- si une interprétation I est un modèle de ψ
alors il existe une interprétation extension de I qui valide ψ' ;
- si une interprétation J valide ψ' alors la restriction de J aux variables de ψ valide ψ.
- Pour ψ :
x1 et ψ', sa transformée
- Pour ψ :
x1 ∨ x2 et ψ', sa transformée
- Pour ψ :
x1 ∨ x2 ∨ x3 et ψ', sa transformée
- Pour ψ :
x1 ∨ x2 ∨ x3 ∨ x4 et ψ', sa transformée
- Pour ψ :
x1 ∨ x2 ∨ x3 ∨ x4 ∨ x5 et ψ', sa transformée
- Pour ψ :
x1 ∨ x2 ∨ x3 ∨ x4 ∨ ... ∨ xl (l ≥ 4) et ψ', sa transformée
- Pour φ CNF quelconque de la forme
ψ1 ∧ ... ∧ ψn et φ' sa transformée
Exercice 5
Le problème du circuit le plus long (longest circuit en anglais, abréviation LC) est le suivant.
Les données sont un graphe G=(V,E), des longueurs l(e) > 0 pour chaque arc e de E et un entier J.
Le problème est de déterminer s'il existe un circuit simple (un chemin fermé ne passant pas deux fois
par le même sommet) pour lequel la somme des longueurs des arcs qui le composent soit au moins J.
Montrer que le problème LC est NP-complet.
Indication : transformation à partir de HC, problème NP-complet (admis).
Exercice 6
Le problème de la clique est le suivant (abréviation CLIQUE). Les données sont un graphe G=(V,E)
et un entier J ≤ |V|. Le problème est de déterminer si le graphe contient une clique de taille au moins égale à J, i.e.
un ensemble de sommets V' tel que |V'| ≥ J et tel qu'il existe un arc de E entre toute paire de sommets
appartenant à V'.
Montrer que le problème de la clique est NP-complet.
Indication : transformation à partir de VC, problème NP-complet (vu en cours). Cf. ce document pour plus de détails.
Exercice 7
Le problème de l'ensemble indépendant (independent set en anglais, abréviation IS) est le suivant.
Les données sont un graphe G=(V,E) et un entier J ≤ |V|. Le problème est de déterminer
s'il existe un sous-ensemble V' ⊆ V de taille J ou plus (|V'| ≥ J) tel que si
u,v ∈ V' alors (u,v) ∉ E.
Montrer que le problème IS est NP-complet.
Indication : transformation à partir de CLIQUE, problème NP-complet (exercice 6) en s'appuyant sur
l'équivalence à justifier : V' est une clique de G=(V,E) ssi V' est un ensemble indépendant de Gc=(V,Ec).
Exercice 8
Ecrire un programme (langage au choix) résolvant un des problèmes suivants :
- le problème HC
- le problème SAT
- le problème VC
Exemple de solution en Prolog pour chacun de ces problèmes
(version en ligne ici).



