No Title

DEUG 1^ere année
MIAS 1 et MASS 1 - Programmation fonctionnelle

TP 7 : Graphisme

L'opérateur de séquentialité : il est parfois nécessaire d'effectuer des actions les unes à la suite des autres dans un ordre fixé. L'opérateur begin dont la syntaxe est : (begin <expr1> <expr2> ... <exprn>) évalue les expressions données en paramètres les unes à la suite des autres et renvoie comme valeur, la valeur de la dernière expressions.
Cet opérateur est utilisé lorsque ce ne sont pas les valeurs des expressions qui importent mais les actions qui sont effectuées. On parle d'effet de bord. C'est le cas avec les fonctions graphiques (ainsi qu'avec les fonctions d'entrée et de sortie) dont les valeurs sont indéfinies mais dont les effets de bords importent.

Exercice 1 :

a): Définir une fonction carre qui prend en argument un entier c et affiche sur la fenêtre graphique un carré centré au point de coordonnées (0, 0), dont le côté et de longueur c.
b): Définir une fonction anime, qui affiche sur la fenêtre graphique un carré centré en (0, 0), de côté 400, et qui diminue progressivement jusqu'à se confondre avec l'origine.

Exercice 2 : Une fractale.
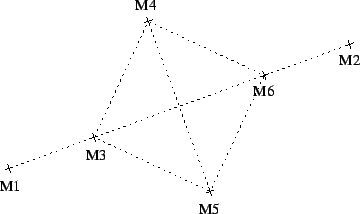
À partir de deux points M₁(x₁, y₁) et M₂(x₂, y₂) du plan, et d'un réel k, on définit les quatre points M₃(x₃, y₃), M₄(x₄, y₄), M₅(x₅, y₅) et M₆(x₆, y₆) tels que :

$\includegraphics{fig2.eps}$

x₃=(3x₁+x₂)/4		y₃=(3y₁+y₂)/4
x₄=[2(x₁+x₂)-k(y₂-y₁)]/4		y₄=[2(y₁+y₂)+k(x₂-x₁)]/4
x₅=[2(x₁+x₂)+k(y₂-y₁)]/4		y₅=[2(y₁+y₂)-k(x₂-x₁)]/4
x₆=(x₁+3x₂)/4		y₆=(y₁+3y₂)/4

La fractale à l'ordre n, à partir des points M₁ et M₂ se construit de la manière suivante :

: si n=0, c'est le segment [M₁, M₂]
: sinon, c'est :
la fractale à l'odre n-1, à partir des point M₁ et M₃ et du réel k,
la fractale à l'odre n-1, à partir des point M₃ et M₄ et du réel k,
la fractale à l'odre n-1, à partir des point M₄ et M₅ et du réel k,
la fractale à l'odre n-1, à partir des point M₅ et M₆ et du réel k et
la fractale à l'odre n-1, à partir des point M₆ et M₂ et du réel k.

Définir une fonction fractale, de paramètres x₁, y₁, x₂, y₂, k et n.
Essayer par exemple (fractale -200 0 200 0 1 3).

Remarque : si on oublie le point M5, on obtient le flocon de Von Koch.

Exercice 3 : Un autre dessin fractal.
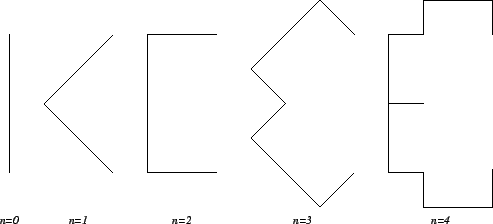
Écrire une fonction dessin, de paramètres x₁, y₁, x₂, y₂ et n, à même de dessiner les figures ci-dessous.

$\includegraphics{fig1.eps}$

On rappelle que les coordonnées de l'angle droit du triangle rectangle isocèle construit dans le sens direct sur A₁(a₁, b₁) et A₂(a₂, b₂) sont (a₁+b₁+a₂-b₂)/2 et (a₂+b₂+b₁-a₁)/2.

Fonctions graphiques simplifiées

Les fonctions qui suivent sont définies à partir des primitives graphiques de DrScheme. Pour les utiliser :

copier le fichier pack-graph.sc dans le dossier où se trouve votre programme,
puis charger ce fichier dans l'environnement global de l'interpète avec la commande (load "pack-graph.sc").

(init-graphics) : ouvre une fenêtre graphique de 600 x 600 points, place l'origine du repère au centre de la fenêtre, et initialise la couleur du crayon en noir.

(init-graphics haut large) : idem mais avec une fenêtre graphique de haut sur large points. (Maximum 600 x 600).

(clear-graphics) : efface le contenu de la fenêtre graphique.

(black-pen) : sélectionne le crayon noir.
(white-pen) : sélectionne le crayon blanc.
(red-pen) : sélectionne le crayon rouge.
(green-pen) : sélectionne le crayon vert.
(blue-pen) : sélectionne le crayon bleu.
(yellow-pen) : sélectionne le crayon jaune.
(orange-pen) : sélectionne le crayon orange.
(purple-pen) : sélectionne le crayon violet.

(set-rgb-color r g b) : affecte au crayon la couleur déterminée par les trois valeurs r, g et b. Ces trois valeurs sont des réels de l'intervalle [0,1] est représentent les quantités de rouge, de vert et de bleu de la couleur.

(position-pen x y) : place le crayon au point de coordonnées (x, y).

(draw-point x y) : dessine le point de coordonnées (x, y) dans la couleur courante du crayon.

(clear-point x y) : efface le point de coordonnées (x, y).

(draw-line-to x y) : trace une ligne depuis la position courante du crayon jusqu'au point de coordonnées (x, y) qui devient la nouvelle position du crayon.