DEUG 1^ere année
MIAS 1 et MASS 1 - Programmation fonctionnelle

TP 6 : Fonctions itératives - Récursivité terminale

Rappel : Le principe général pour écrire des fonctions itératives consiste à introduire une fonction auxiliaire dont un paramètre dit compteur permet de compter les étapes du calcul et dont le ou les autres paramètres, dits accumulateurs, sont utilisés pour mémoriser les calculs en cours.
Lorsque la valeur du paramètre compteur atteind sa valeur d'arrêt, le résultat de la fonction doit être obtenu directement par la valeur d'un des paramètres accumulateurs ou bien par un calcul simple portant sur ces paramètres.
On passe d'une étape du calcul à la suivante en mettant à jour le compteur de manière à ce qu'il se rapproche de sa valeur d'arrêt et en mettant à jour les valeurs des accumulateurs.
On dit d'une fonction récursive qu'elle est récursive terminale si le résultat de l'appel récursif n'est pas utilisé comme argument d'une autre fonction.

Exercice 1 : Écrire une version itérative de la fonction :

puissance :	Reel+, Entier	$\rightarrow$	Reel+
	x , n	$\mapsto$	xn

Exercice 2 : Étant donnés deux entiers a et b, on veut calculer la somme $S(n)=\sum_{i=0}^{n} a^i b^{n-i}$ qu'on peut définir par récurrence :

$$\left\{\begin{array}{ll} S(0)=1\\ S(n)= a^n + b S(n-1) & \forall n \geq 1 \end{array}\right.$$

a.

Écrire une fonction récursive directement inspirée de la définition par récurrence ci-dessus.

b.

Écrire une fonction récursive terminale calculant S(n)

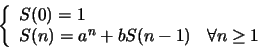
Exercice 3 : Écrire une fonction récursive terminale permettant de calculer $S(n)=\sum_{i=1}^{n}\frac{1}{n!}$ sans utiliser de fonction calculant la factorielle.

Exercice 4 : Écrire une fonction récursive terminale qui permet de renverser une liste.

Exercie 5 : Écrire une fonction récursive terminale qui compte le nombre d'occurences d'un élément dans une liste.

Exerccie 6 : Écrire une fonction itérative qui effectue la concaténation de deux listes.

Exercice 7 : Calcul de $\pi$.
Afin de calculer une valeur approchée de $\pi$, on utilise la somme infinie suivante :

$$\frac{\pi}{8} = \frac{1}{1.3} + \frac{1}{5.7} + \frac{1}{9.11} + \ldots + \frac{1}{i(i+2)} + \frac{1}{(i+4)((i+4)+2)} + \ldots$$

Considérons la suite u suivante :

$$\left\{\begin{array}{ll} u(0)= 0\\ u(n)= \frac{1}{n(n+2)} & \forall n \geq 1 \end{array}\right.$$

La somme ci-dessus sécrit aussi :

$$\frac{\pi}{8} = u(1) + u(5) + u(9) + \ldots + u(i) + u(i+4) + \ldots$$

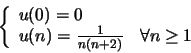
Écrire une fonction itérative permmettant de calculer la somme des n premiers termes de la somme infinie donnant $\frac{\pi}{8}$.