MIAS 1 et MASS 1 - Programmation fonctionnelle

TD 9

But : se familiariser avec la programmation d'ordre supérieur.

I) Fonctions en paramètres.

Exercice 1 : La fonction prédéfinie map.

A) Évaluer les expressions suivantes :

     (map cdr '((2 3 4)(5 6)(a b c)))                (map integer? '(1 a 3 0.75 (2 4)))

     (map cons '(2 3 4) '(5 6 7))                    (map (lambda (x y) (if (= x y) 1 0))
                                                          '(2 3 4 1 2 2 1)
                                                          '(7 3 5 1 2 0 3))

B) En utilisant la fonction map, écrire une expression qui transforme la liste de paires pointées
((1 . 2)(3 . 4)(5 . 6)) en ((2 . 1)(4 . 3)(6 . 5)).

Exercice 2 :
A) Spécifier et écrire une fonction qui permet de calculer la somme $\sum_{i=1}^{n}f(i)$, f étant une fonction entière quelconque.

B) Quelle expression évaluer pour calculer $\sum_{i=1}^{100}\frac{1}{i}$ ?

II) Fonction comme résultat.

Exercice 3 : Valeur approchée de l'intégrale d'une fonction.

On peut obtenir une valeur approchée de l'intégrale d'une fonction réelle (supposée intégrable) f sur un intervalle [a, b] en calculant l'aire algébrique de la surface délimitée par l'axe des abscices, la courbe repésentative de f et les droites y=a et y=b, c'est à dire l'aire hacurée du dessin ci-dessous à gauche. Calculer une valeur approchée de $\int_{a}^{b}f$ revient donc à calculer une valeur approchée de cette aire.

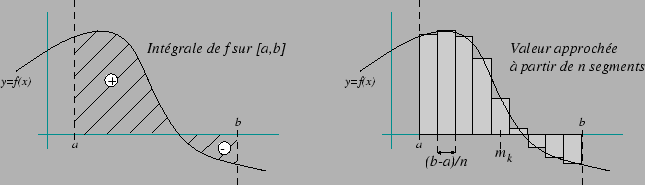
Pour calculer une valeur approchée de l'aire, on découpe l'intervalle [a, b] en n segments de longueur (b-a)/n et on calcule la somme des surfaces de n rectangles dont les largeurs sont égales à (b-a)/n et les hauteurs sont données par les valeurs de f au milieu de chaque segment (dessin de droite).

L'abscice du milieu du ksegment est $m_k=a+(k-1)\frac{b-a}{n} + \frac{1}{2}\frac{b-a}{n}$ (abscice du début du ksegment augmentée de la moitié de la longeur d'un segment).

L'aire du krectangle A_k est donc $A_k=\frac{b-a}{n}\times f(m_k)$

Pour un nombre de rectangles n, la valeur approchée de l'intégrale $\int_{a}^{b}f$ est donc donnée par la somme :

$$\sum_{k=1}^{n}A_k=\frac{b-a}{n}\times \sum_{k=1}^{n}f(m_k)$$

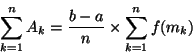
Écrire la fonction integrale qui prend comme paramètres une fonction f et un nombre de rectangles n et renvoie comme résultat une fonction qui calcule la valeur approchée de l'intégrale de f entre deux bornes a et b. La spécification de cette fonction est :

integrale :	Fonction,	Entier	$\longrightarrow$	Fonction
	f	n	$\longmapsto$	$a, b \longmapsto \sum_{k=1}^{n}A_k$

Pour écrire cette fonction on utilisera la fonction somme définie dans l'exercice précédent.