3.1 La méthode:

Définir le problème à résoudre :
        Expliciter les données : préciser leur nature, leur domaine de variation, leur propriétés.
        Expliciter les résultats : préciser leur structure, les relations entre les données et les résultats.

Décomposer le problème en sous problèmes ;

Pour chaque sous problème P faire :
        Si P a une solution immédiate
            alors écrire le morceau de programme correspondant
            sinon appliquer cette méthode à P ;

3.2 Exemple : faire une lessive.

Pour faire une lessive :
    1 : introduire le linge sale et la lessive dans la machine, sélectionner les options.
    2 : mettre la machine en marche et attendre l'arrêt de celle-ci.
    3 : sortir le linge propre.

Mais si le programmateur est en panne ?
Supposons qu'il soit possible de commander manuellement les divers composants de la machine et effectuons un premier niveau d'analyse :

Pour faire une lessive :
    1 : introduire le linge sale et la lessive.
    2 : laver.
    3 : rincer.
    4 : si on désire un essorage, alors essorer.
    5 : sortir le linge propre.

Il nous faut à présent détailler les étapes 2, 3 et 4.

Pour le module 3 "rincer", un deuxième niveau d'analyse peut conduire à :
rincer :
    3.1 : remplir la cuve.
    3.2 : remuer le linge.
    3.3 : vider la cuve.

Affinons (troisième niveau d'analyse), le module 3.1 :
remplir la cuve :
    3.1.1 : ouvrir le robinet d'arrivée d'eau.
    3.1.2 : tant que la cuve n'est pas pleine, surveiller le niveau d'eau.
    3.1.3 : fermer le robinet d'arrivée d'eau.

A présent, on peut considérer que les actions à effectuer sont élémentaire ( i.e. appartiennent à l'ensemble des commandes manuelles disponibles de la machine) et que le sous problème 3 "rincer" a été complètement décomposé. Il resterait à analyser de la même façon les étapes 2 et 4.

Dès que la complexité du programme à programmer dépasse un certain seuil, la méthode d'analyse fait apparaître une décomposition de l'algorithme en "modules" que nous coderons par des sous-programmes.

Ces sous-programmes seront utilisés par d'autres sous-programmes ou programmes :

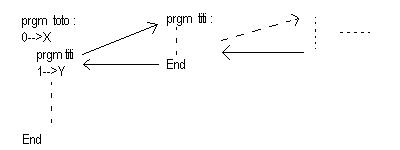
La mémoire de la machine, pour les variables est globale à toutes les zones de programmes.
Donc, pour chaque sous-programme il convient de spécifier les variables en entrée,  les variables en sortie et les variables modifiées par le sous-programme.

Lorsque dans le programme 1, P1, on souhaite appeler le programme 2, P2,  on procède comme suit :
    1/ sauvegarder les variables de P1 dont on sait qu'elles seront modifiées par P2.
    2/ préparer l'appel en affectant les variables en entrée à P2.
    3/ appeler P2.
    4/ sauvegarder les variables en sortie de P2.
    5/ restituer les valeurs des variables de P1 sauvegardées en 1/

Exo 1: Soient n et p deux entiers non nuls.
          Ecrire un sous-programme qui détermine le plus grand entier i tel que p^i  (i.e. p à la puissance i) divise n.

Exo 2 : Soit p un entier >=2. Ecrire un sous-programme qui détermine si p est premier.

Exo 3 : Soit p un entier. Ecrire un sous-programme qui détermine le plus petit nombre premier>p.

Exo 4 : Soit n un entier. A l'aide des sous-programmes définis précédemment, écrire un programme qui
            affiche la décomposition de n en facteurs premiers.