Chapitre 1:   PL un pseudo langage permettant d'exprimer des algorithmes
 

1.1 Les objets élémentaires manipulés par PL

 a / les nombres
                         valeur
Exemple:      10  ------>  10
                    2.5 ------> 2.5
auxquels on associe les opérateurs arithmétiques usuels: -, +, *, /.
Exemple:      2+3*4 ------>14
 
b / les booléens

Exemple:   vrai ------> vrai
                faux ------> faux
auxquels on associe les opérateurs booléens usuels: non, et, ou:
 

   a    b      non(a)        a et b         a ou b
et les tests arithmétiques: =,#, >, >=, <, <=.

Exercice:   vrai et non(faux) ------>
                      1>2              ------>
                 1>2 ou 1<2       ------>

1.2 Identificateurs et mémoire
 a /  Un identificateur est un nom, i.e. une suite de lettres et de chiffres, référençant une variable.
Exemple:   i1
                test
                surface
                somme

b / La mémoire est un tableau qui à tout identificateur associe un nombre ou un booléen.

Exemple:  
i1 20
test vrai
surface 10
somme 256
 
Nous pouvons maintenant considérer des expressions arithmétiques ou booléennes où figurent des identificateurs et les évaluer.
Exercice:      
                                       M
                 2 * i1            ------> 40
          non(test ou faux)   ------>
         somme-surface/10  ------>
                     toto            ------> erreur variable non définie
 

1.3 Les trois instructions élémentaires de PL
 
a / L'affectation remplace la valeur précédente de la variable (si elle existait) par une nouvelle valeur.

Exemple:
 
test vrai   test <-- faux  test faux
mémoire avant                                              mémoire après
affectation                                                     affectation
 
 __  __   toto <-- 2  toto   2 
 
Syntaxe: <identificateur>  <--  <expression>
Sémantique: <expression> est évaluée relativement à l'état de la mémoire avant affectation puis la mémoire
                   mise à jour.
Exercice:
 
i1 20 i1 <-- i1+somme i1 ___ 
somme 256 somme  
b / Entrée d'une donnée : lecture d'une valeur entrée au clavier et affectation à une variable.

Syntaxe: Lire [message] <identificateur>
Sémantique: un nombre ou un booléen est lu du clavier puis affecté à la variable référencée par <identificateur>.
Exercice:
 
n 10 lire n     3 n 3
lire n     3
c / Écriture de la valeur d'une expression.

Syntaxe: Afficher [message] <expression>
Sémantique: <expression> est évaluée relativement à l'état courant de la mémoire puis affichée à l'écran.
Exemple:
n 3 Afficher  n*3   n 3
 

1.4 Les trois structures de contrôle de PL
a / La séquence

Syntaxe: <instruction 1>;
              <instruction 2>
Sémantique: Mo exécution de l'instruction 1   M1
                   M1 puis exécution de l'instruction 2   M2
Exemple: Lire "entrer n" n ;
               p <-- 2*n+1

b / L'alternative
 
Syntaxe:                                                                    Sémantique:

* si <condition>                                              <condition> est évaluée .Si sa valeur est vraie ,alors
         alors <séquence>                                   <séquence>  est exécutée.
   finsi
         * si <condition>                                               <condition> est évaluée .Si sa valeur est vraie ,alors
                 alors <séquence 1>                                  <séquence1>  est exécutée sinon
                sinon <séquence 2>                                  <séquence 2>  est exécutée.
           finsi
Exemple:
Lire  X;
si X>=0                                                           Que réalise le programme suivant?  
           alors sgn  <--  vrai ;
                       Y <-- X;
           sinon sgn <-- faux;  
                     Y  <--  -X;
finsi;
Afficher Y;
Afficher sgn
c / La boucle tant que....faire

Syntaxe:                                                                   Sémantique:
             tant que <condition> faire                             1: <condition> est évaluée.
                             <séquence>                                 Si sa valeur est vraie ,<séquence> est exécutée
             fin tant que                                                     et on retourne en 1 avec l'état de la mémoire
                                                                                 résultant de l'exécution de   <séquence>.
                                                                                 Si sa valeur est fausse, on passe à l'instruction
                                                                                 qui suit le  fin tant que.

Exemple: Lire X
              tant que X>0  faire
                     Afficher 2/X;
                     Lire X;
              fin tant que

1.5 Les organigrammes (ou ordinogrammes)

Les organigrammes sont une représentation graphique des programmes. On distingue quatre schémas de base:

 
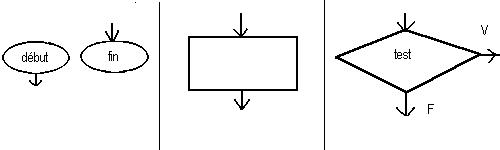                             étiquettes de début et fin             Bloc, i.e. séquences              conditionnelle
                                                                             d'affectation et E/S                (si...alors...sinon)
 
Les schémas de base sont reliés entre eux par des arcs fléchés.
  Exemple 1:
 
 
 
 
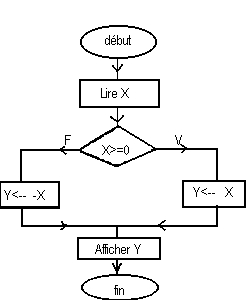
      Lire X;
        si X>=0
            alors Y<-- X

            sinon Y<--  -X
        finsi;
    Afficher Y;
 
 
 
 
 

Exemple 2:

 

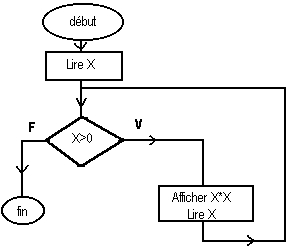
     Lire X;
        tant que X>0 faire
            Afficher X*X;
            Lire X;
        fin tant que;
 
 
 
 
 

On démontre que les organigrammes et le langage PL ont la même puissance d'expression:
       - Pour tout P programme de PL, il existe Pi organigramme tel que Pi=P  (facile)
       - Pour tout Pi organigramme, il existe P programme de PL tel que P=Pi   (difficile).

Intérêts des organigrammes:
       - représentation visuelle du contrôle (suivre les flèches),
       - facilite l'écriture des programmes dans un langage de bas niveau (type calculette).

MAIS dangereux: des flèches partout, qu'on modifie sans bien réaliser les conséquences induites.
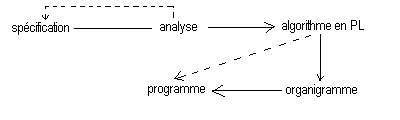
D'ou la démarche préconisée:

1.6 Exemples de programmes en PL
 

a /  Écrire un programme qui demande à l'utilisateur d'entrer la longueur et la largeur d'un rectangle et qui affiche sa surface.
Analyse: -entrée des données
             -calcul de la surface
             -affichage du résultat
d'où

    Afficher "Entrer la longueur:  ";
    Lire longueur;
    Afficher "Entrer la largeur:  ";
    Lire largeur;
    surface <-- longueur * largeur;
    Afficher "la surface:  ";
    Afficher surface;

b / Que réalise les 3 affectations suivantes ?:
            X <-- X+Y;
            Y <-- X-Y;
            X <-- X-Y;

c / Écrire un programme qui demande d'entrer deux nombres et affiche le plus grand.

Analyse: -entée de X et Y
              -recherche du max.: si X>=Y alors max<--X
                                                          sinon max<--Y
d'où

    Afficher "Entrer un nombre:  ";
    Lire X;
    Afficher "Entrer un nombre:  ";
    Lire Y;
    si X>=Y alors max<--X
                  sinon max<--Y;
    finsi;
    Afficher "Le max. est:  ";
    Afficher max.;
 

d / Une fois le programme suivant exécuté, quelle relation existe-t-il entre Z (booléen), X et Y (nombres)?
    Lire X;
    Lire Y;
    si X=0 ou Y=0
        alors Z<-- vrai
        sinon si X>0
                        alors si Y>0
                                        alors Z<-- vrai
                                        sinon Z<-- faux
                                finsi
                        sinon si Y<0
                                        alors Z<-- faux
                                        sinon Z<-- vrai
                                finsi
                finsi
    finsi;
e / Écrire un programme après lecture d'un entier n>=0, calcul puis affiche la somme des n premiers entiers 1+2+...+n-1+n.
    Lire n;
    somme<--0;
    compteur<--0;
    tant que compteur<n faire
                compteur<--compteur +1;
                somme<-- somme+compteur;
    fin tant que;
    Afficher somme;

Remarque: dès qu'il y a une boucle tant que ou répéter, s'assurer de la terminaison du programme.
        Ici: compteur est initialisé à 0 puis augmente par pas de 1 donc au bout d'un nombre fini d'itérations la condition
             compteur<n est fausse.

f / Modifier le programme e /  pour calculer S=1+2²+3²+...+(n-1)²+n².

g / Le programme proposé comme solution de l'exercice e / ne vérifie pas que le nombre entré est bien entier >=0 .Voici une façon d'effectuer ce contrôle (Int est la fonction partie entière).

    répéter
        Afficher "Entrer un entier positif:  ";
        Lire n;
    jusqu'à (n>=0) et (n=Int(n));
On considère la suite d'entiers (Un) définie par:
    Uo=0
    U1=1
    Un+2=Un+1  + Un  pour n>=0
Proposer un programme qui, après lecture de d'un entier n>=0, calcule puis affiche le terme Un.

h / Proposer un programme qui, après lecture de deux entiers strictement positifs calcule et affiche leur pgcd (cf. algorithme d'Euclide).

i / Proposer un programme qui après lecture d'un entier n >=0 calcule puis affiche n! (sans utiliser la fonction ! ,si elle est disponible).

j / Proposer un programme qui, après lecture de deux entiers n et p tels que n>=p>=0, calcule puis affiche:  (n! p!) / (n-p)!

k / Pour chacun des programmes a / à j / déterminer l'organigramme équivalent.