Exercices NP-complétude

Exercice 1

Soient f, g et h trois fonctions de N dans N, avec f(n) et g(n) en O(h(n)).

Montrer que f(n)+g(n) est une fonction en O(h(n)).
Montrer que f(n)*g(n) est une fonction en O(h(n)²).

Exercice 2

Déterminer la complexité en temps de la MTD M1 :
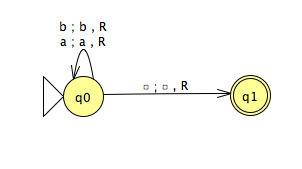
Déterminer la complexité en temps de la MTND M2 :

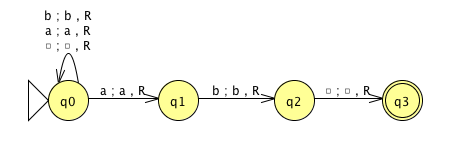
Exercice 3

Les documents relatifs à cet exercice se trouvent dans ce répertoire.

Se familiariser avec la syntaxe DIMACS des formules CNF
Le principe des tiroirs est un test classique pour un solveur propositionnel car le nombre d'étapes pour la résolution propositionnelle est exponentielle en fonction du nombre de chaussettes. Modéliser et résoudre pour 2, 3 et 4 chaussettes. Généraliser à n chaussettes et tester SATJ pour n compris entre 2 et 50.
Résoudre à l'aide de SATJ les exercices de la fiche tp-sat

Exercice 4

Soient L1 et L2 deux langages appartenant à la même classe de complexité P ou NP. Quelle est la classe de complexité des langages L1 ∩ L2 et L1 ∪ L2 ? Et que dire si L1 et L2 sont dans NPC ?

Exercice 5

Soit L un langage, on note L son complément. On définit co-NP comme la classe des langages L tels que L est dans NP.

Montrer que le problème de décider si une formule booléenne est valide (toujours vraie) est dans co-NP
Montrer que P est contenu dans co-NP
Montrer que si L1 α L2 alors L1 α L2
Montrer que si L1 α L2 et L2 dans NP alors L1 dans NP
Montrer que s'il existe un langage NP-complet L0 que L0 soit dans co-NP, alors NP = co-NP

Exercice 6

Le problème de la clique est le suivant (abréviation Clique). Les données sont un graphe G=(V,E) et un entier J ≤ |V|. Le problème est de déterminer si le graphe contient une clique de taille au moins égale à J, i.e. un ensemble de sommets V' tel que |V'| ≥ J et tel qu'il existe un arc de E entre toute paire de sommets appartenant à V'.
Montrer que le problème de la clique est NP-complet. Indication : transformation à partir de VC.

Exercice 7

Le problème de l'ensemble indépendant (independent set en anglais, abréviation IS) est le suivant. Les données sont un graphe G=(V,E) et un entier J ≤ |V|. Le problème est de déterminer s'il existe un sous-ensemble V' ⊆ V de taille J ou plus (|V'| ≥ J) tel que si u,v ∈ V' alors (u,v) ∉ E.
Montrer que le problème IS est NP-complet. Indication : transformation à partir de Clique.

Exercice 8

Le problème du circuit le plus long (longest circuit en anglais, abréviation LC) est le suivant. Les données sont un graphe G=(V,E), des longueurs l(e) > 0 pour chaque arc e de E et un entier J. Le problème est de déterminer s'il existe un circuit simple (un chemin fermé ne passant pas deux fois par le même sommet) pour lequel la somme des longueurs qui le composent soit au moins J.
Montrer que le problème LC est NP-complet. Indication : transformation à partir de HC, dont nous admettons la NP-complétude.

Exercice 9

Appliquer à la main un algorithme polynomial (cf. Wikipedia) pour déterminer la satisfiabilité des formules suivantes :

(x ∨ y) ∧ (x ∨ ¬ z) ∧ (¬ x ∨ y) ∧ (y ∨ z)
(x ∨ y) ∧ (z ∨ ¬ t) ∧ (x ∨ t) ∧ (x ∨ z) ∧ (¬ y ∨ t)

Exercice 10

Ecrire un programme de complexité polynomiale (langage au choix) résolvant 2-SAT (cf. Wikipedia).

Exercice 11

Ecrire un programme (langage au choix) résolvant un des problèmes suivants :

le problème HC
le problème SAT
le problème VC