Exercices MT et JFLAP
- JFLAP
- Copie locale
- MTD = machine de Turing déterministe
- MTND = machine de Turing non-déterministe
- Σ={a,b}
Exercice 1
Soit L l'ensemble des mots construits sur Σ qui se terminent par au moins un a.
- Définir une MTD M1 qui décide L.
- Définir une MTD M2 qui accepte L mais ne le décide pas.
Dans chacun des cas, justifier. Tester avec JFLAP.
Exercice 2
Donner une définition aussi simple que possible d'une MTD M
telle pour tout mot d'entrée w construit sur Σ, l'exécution de M sur w est
une suite infinie de configuration. Tester avec JFLAP.
Exercice 3
Considérer la MTD M1 :
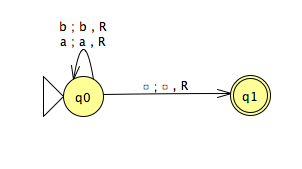
- Définir formellement M1=(Q, Γ, Σ, δ, s, B, F).
- Justifier la terminaison de M1 pour tout mot d'entrée.
- Quel est le langage décidé par M1 ?
- Construire M1 à l'aide de JFLAP.
- Tester M1.
Exercice 4
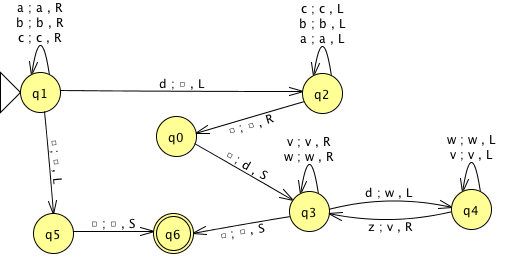
Considérer la MTD M2 :
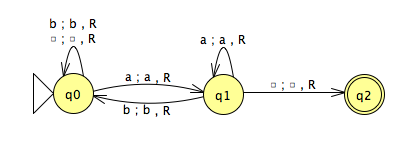
- Construire M2 à l'aide de JFLAP.
- Existe-t-il des mots qui génèrent une exécution infinie de M2 ? Le constater.
- M2 peut-elle décider un langage ?
- Quel est le langage accepté par M2 ?
- Modifier M2 pour qu'elle décide ce langage.
Exercice 5
Soit la machine de Turing M=(Q, Γ, Σ, δ, q0, #, Ø) avec :
- Q={q0, q1, q2, q3},
- Γ={a, b, A, A', B, B', #},
- δ définie par :
| (q0,a) → (q1,A',R) |
(q0,b) → (q3,B',R) |
| (q1,a) → (q1,a,R) |
(q3,a) → (q3,a,R) |
| (q1,b) → (q1,b,R) |
(q3,b) → (q3,b,R) |
| (q1,A) → (q1,A,R) |
(q3,A) → (q3,A,R) |
| (q1,B) → (q1,B,R) |
(q3,B) → (q3,B,R) |
| (q1,#) → (q2,A,L) |
(q3,#) → (q2,B,L) |
| (q2,a) → (q2,a,L) |
(q2,b) → (q2,b,L) |
| (q2,A) → (q2,A,L) |
(q2,B) → (q2,B,L) |
| (q2,A') → (q0,A,R) |
(q2,B') → (q0,B,R) |
- M est-elle déterministe ou non-déterministe ? Justifier.
- Donner la suite des configurations de M obtenues pour le mot d'entrée abb.
- Quel est le contenu du ruban après exécution de M sur le mot abab ?
- Vérifier ces deux derniers résulats avec JFLAP.
Exercice 6
Construire une MTND
à 4 états qui accepte les mots de Σ* se terminant par ab.
Dessiner les arbres d'exécutions pour le mot vide, a, ab, aba et bab.
Exercice 7
Construire une MTD qui calcule l'application f(n)=2n, où
les entiers sont codés :
- en notation binaire ;
- en notation unaire.
Exercice 8
On peut définir des machines de Turing qui ont la possibilité supplémentaire
d'écrire un symbole sans modifier la position de la tête de lecture.
- Définir la relation de dérivation entre configurations pour ces machines
(cf. la page 57 du support de cours).
- Expliquer comment compiler de telles machines en machines de Turing standards.
- Appliquer à la machine ci dessous.